 |
Temas: Matemáticas. Naturaleza. Arte. Mapa del sitio. Mail. |
 |
La
espiral equiangular o logarítmica.
Curvas asociadas.
Curvas de Busqueda
Las curvas de busqueda son el rastro de un objeto que persigue otro.
Suponga que hay
insectos, cada uno en
una esquina de un
polígono
regular de caras. Cada insecto se arrastra hacia su vecino
siguiente
con velocidad uniforme. El rastro de estos insectos son espirales
equiangulares de ángulo 
radianes
(que es la mitad del ángulo de la esquina del
polígono). Si suponemos que este rastro es una espiral
equiangular, es natural que sea una de
radianes,
ya que una tangente a la espiral resulta ser un lado del
polígono. |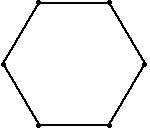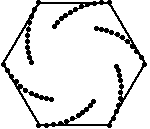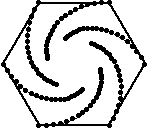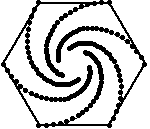
 |
 |
 |
 |
 |
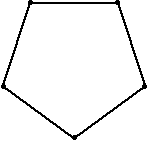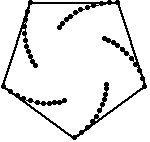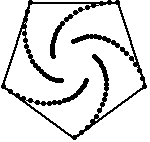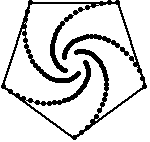
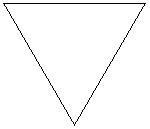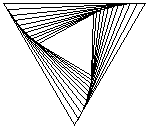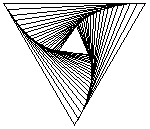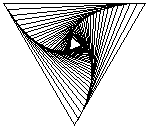
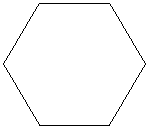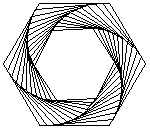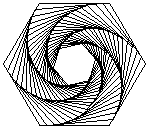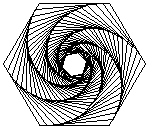
Las figuras de arriba muestran el rastro de los insectos que se persiguen, resultando espirales de 60, 45 y 54 grados respectivamente. Las figuras de abajo muestran también las lineas de dirección de cada insecto, podemos apreciar que cada línea es tangente a los espirales y forma parte un polígono semejante al original, luego, la espiral formada debe ser una equiangular.
Consideremos ahora que el lado del polígono mide una unidad y se divide en
partes siendo
un número entero. Supongamos que los puntos
recorren
una de esas -ésimas
partes como una aproximación de su
trayectoria, y
que de esta manera quedan nuevamente en los vértices de un
polígono
regular, pero contraído, como se muestra en las figuras,
más arriva.Aplicando la ley de cosenos:
Donde
es el nagulo de un
vértice del polígono regular y 
es el lado del
nuevo
polígono regular formado.En esta ecuación
resulta
ser también la razón entre el lado original de
polígono con el
nuevo lado una vez que los puntos han recorrido una
aproximación (ya que el lado original es de largo 1), de
acuerdo a una fija.De esa manera, la longitud
recorrida se representa por
la suma infinita:
La cual es convergente ya que necesariamente
es menor estricto que 
.
Luego como es clásico, el límite de esta suma es:
Sustituyendo a
en la
espresión anterior obtenemos :
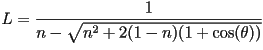
Esta distancia sigue siendo aproximada. Para obtener la verdadera,
debe volverse infinita y comon-\sqrt{n^2 + 2(1-n)(1 + \cos(\theta))}= n-\sqrt{ (n-(1+\cos(\theta)))^2 + (1 +\cos(\theta))(1-\cos(\theta)) }
al tomar el límite obtenemos que :
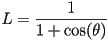
En el caso de un triángulo equilatero
y por tanto cada punto
en el triángulo
recorre 
de la distancia
que originalmente los separaba. Si fuesen
cuatro puntos ubicados en un cuadrado recorrerían hacia el
centro
exactamente la misma distancia que los separaba.Por último, señalemos que éste método nos dá otra demostración de que la longitud de arco
de una curva
como la dada por 
está determinada por 
y el lado del polígono regular (debido a la ley
del coseno) está dado por 
.Luego
lo que prueba la formula de
obtenida en la sección
anterior.Este problema fue resuelto en gran medida gracias a :
Octavio Alberto Agustín Aquino.
Universidad Tecnológica de la Mixteca, Oaxaca, México.
Correo: octavioalberto.geo@yahoo.com
URL:www.geocities.com/octavioalberto.geo/indice.html.
Evoluta e Involuta de la espiral equiangular
Recordemos que la evoluta es un método de derivar una curva nueva basandose en una curva dada. Este método consiste en describir el lugar geométrico de los centros de los círculos definidos por los radios de curvatura de la curva dada (ver sección 6.3.2). Análogamente, como la involuta es la operación inversa de la evoluta, obtendremos que si la evoluta de una espiral equiangular es otra espiral equiangular, entonces la involuta también.
La evoluta de una espiral equiangular se puede apreciar graficamente en la siguiente animación, donde se ha dibujado la espiral equiangular inicial
con una linea
negra, luego, se han dibujado sus normales (lineas azules) para
apreciar la ubicación de los centros de los circulos de curvatura (de color rojo). Se
puede apreciar que la evoluta 
(de color rojo), de una
espiral equiangular (de color negro), resulta ser
también una espiral equiangular.
Como sabemos, un espiral equiangular, puede estar dado en forma paramétrica por
 |
 |
 |
 |
Luego, la evoluta está dada paramétricamente por
 |
 |
 |
 |
Y entonces, analíticamente, la evoluta de un espiral equiangular es otra espiral equiangular, con parametros
y 
.En algunos casos, la evoluta es idéntica a la espiral original, como puede ser demostrado haciendo la substitución en la nueva variable:
.Entonces las ecuaciones anteriores se convierten en :
|
 |
 |
 |
|
 |
|
 |
las que son equivalentes a la forma de la ecuación original si se verifica que
.Envoltura de la espiral equiangular
[ojo, no confundir envoltura con evoluta aunque en el caso de la espiral equiangular "coincidan"]
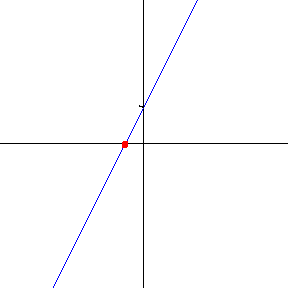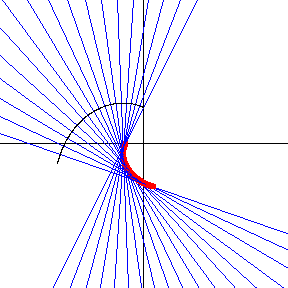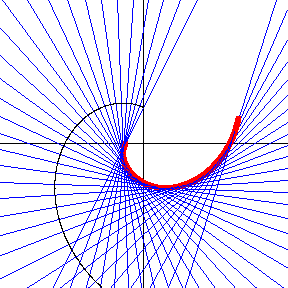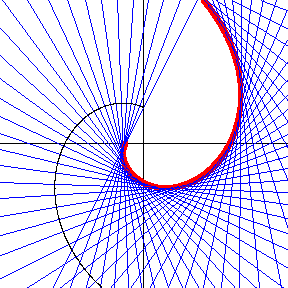
Recordemos que, la envoltura es un método de derivar una curva nueva basandose en un conjunto de curvas.
Dada ahora una espiral equiangular (de color negro), y consideramos la familia de rectas normales a ella (familia de color azul), obtenemos que la envolvoltura de esta familia no es ni más ni menos que la evoluta de la espiral negra, es decir, para una espiral equiangular arbitraria, su evoluta y la envoltura de su familia de curvas normales coinciden, como se aprecia en la siguiente figura
Cáustica de la espiral logarítmica
Recordemos que la cáustica es un método de derivar una curva nueva basandose en una curva dada y un punto llamado fuente.
Para una espiral equiangular (color azul), se puede ver en la siguiente figura, que su cáustica (espiral roja), es nuevamente una espiral equiangular.
La inversa de la espiral equiangular
Recordemos que la inversa es un método de derivar una curva nueva basandose en un circulo llamado polo.
Si tomamos como curva a una espiral equiangular azul y como polo a un circulo amarillo centrado en el origen e invertimos la curva con respecto al polo, como se muestra en la siguiente figura
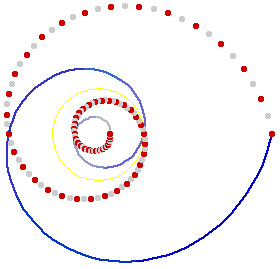
obtendremos nuevamente una espiral equiangular, formada con los puntos de colores.
La podaria
Recordemos que la podaria y la podaria negativa es un método de derivar una curva nueva basandose en una curva dada y un punto llamado polo.
Si tomamos entonces, como curva a una espiral equiangular azul y como polo al origen, como se muestra en la figura
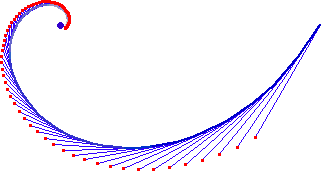
obtenemos nuevamente una espiral equiangular, formada con los puntos rojos, los cuales tienen la propiedad de que la linea que va desde el polo hasta cualquier punto rojo es perpendicular a la tangente que pasa por el mismo (lineas azules).
Radial
Recordemos que la radial es un método de derivar una curva nueva basandose en una curva dada y un punto llamado polo.
Si tomamos entonces, como curva a una espiral equiangular azul y como polo al origen, como se muestra en la figura
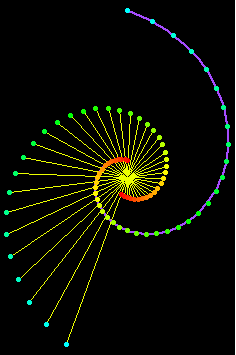
obtendremos nuevamente una espiral equiangular, formada por los puntos verdes.
La parte radial de una espiral equiangular con respecto a su origen es la misma espiral escalada.
En efecto la radial de una espiral equiangular con respecto a su origen está dada por la ecuación
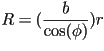
donde
es el ángulo de la espiral equiangular dada
por 
, y con lo cual se ve claramente que el factor de
escalamiento está dado
por 
.
