 |
Temas: Matemáticas. Naturaleza. Arte. Mapa del sitio. Mail. |
 |
Curvas
de una Curva Plana.
Inversa.
La inversa es un método de derivar una curva nueva basada en un círculo. Es por tanto una transformación independiente de la curva, que consiste en aplicar la transformación a cada punto de la curva a transformar, la transformación es naturalmente, la poputal inversión, que a todo geómetra ha cautivado, ya que con ella se puede definir una nueva geometría muy particular e interesante.
Recordemos entonces, la transformación llamada inversión:
Dado un circulo arbitrario y fijo
, un
par de puntos 
y 
se dice que son mutuamente
inversos con respecto a
si la recta que los une 
corta el círculo
en forma perpendicular una única vez y cumplen la ecuación
donde
es
el centro del círculo, 
es el radio del
círculo y 
es la distancia entre 
y 
. Y se dice entonces que es la
inversión de con respecto a .De esta definición, se obtienen inmediatamente dos propiedades:
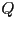- es
la inversión de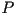
si y solamente si
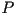es la
inversión de .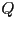
- Los puntos de dentro del círculo son mapeados al exterior y viceversa.
Cuando
se aleja de ,
su inversión se acerca a . De esta
observación, podemos entonces definir la inversión de
como un punto
en el infinito y viceversa. Con tal definición, hemos obtenido
una
transformación en un plano
con un punto en el infinito,
a este plano con el punto en el infinito se le llama Proyección
Estereografica y es un concepto muy importante en
geometría. Se
demuestra que tal plano es topológicamente
equivalente a una esfera (posada encima del plano), que dos rectas
siempre se intersectan en el infinito, etc.
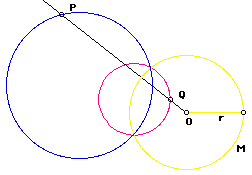
En la figura anterior, el círculo azul es la inversión del círculo rojo con respecto al círculo amarillo y viceversa.
La inversión de una curva es la inversion de todos los puntos de la curva y la curva nueva formada se denomina inversa de la curva original.
Es directo de las propiedades que, si la curva
es la inversa de la
curva
, entonces
la curva
es también la inversa de la curva , obviamente que
con
respecto al mismo círculo ambas inversiones. Al círculo de la inversión se le llama el polo.
Una característica, que se desprende fácilmente de la definición, es que el radio del círculo de la inversión afecta la escala de la curva inversa, pero no afecta su forma. Las curvas cuya inversion son ellas mismas se llaman las curvas anallagmaticas.
Los círculos, las líneas, y los óvalos de Cassinian son curvas anallagmaticas.
Para encontrar la inversión de una curva
con respecto a
un círculo 
de radio
y centro
se puede proceder de la siguiente forma: - Dibuje la recta
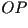para
algún punto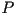
de la curva. - Marque el punto 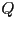de esta recta
que cumpla con la ecuación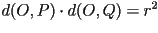
- Repita esto para otros
puntos
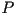de la curva.
es la
inversion de la curva con respecto
al círculo
