 |
Temas: Matemáticas. Naturaleza. Arte. Mapa del sitio. Mail. |
 |
La
espiral equiangular o logarítmica.
Propiedades.
Decididamente cuesta trabajo a la hora de decidirse por uno de los tres nombres de la espiral. Cada uno de ellos la define matemáticamente de forma precisa, mediante una de sus propiedades.
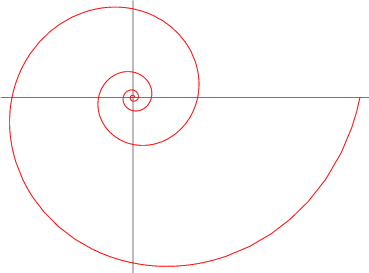
Recordemos que la espiral logarítmica es un espiral que sigue una ecuación polar:
donde
y 
son
constantes, 
es la base nepiriana de los lógaritmos
naturales, 
el radio de posición de un punto y 
el ángulo girado desde el eje 
medido en
contra de las manecillas del reloj.Paramétricamente, en coordenadas cartesianas:
 |
 |
 |
 |
La tasa de cambio del radio con respecto al ángulo se obtiene derivando su ecuación polar y está dada por
 |
 |
 |
 |
con esto y la siguiente figura
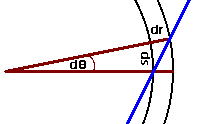
podemos deducir que la tangente del ángulo entre la tangente a la curva (linea azul) y la línea radial en el punto
está dada
por
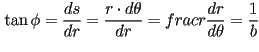
luego, tenemos una expresión para este ángulo:
el cual, como vemos es constante y se llama ángulo de la espiral equiangular, o dicho de otra manera la curva dada por
.Así pues, si
tiende a 
,
tenderá a 
y por tanto la espiral
tiende a un
círculo de radio 
, como también se
puede apreciar tomando este límite en su ecuación polar.Su ecuación polar, en función de \phi queda entonces de la siguiente forma:
La expresión de \phi en función de b también se puede obtener de una forma más analitica y no tan intuitiva, para ello lo primero que debemos encontrar es una expresión para la tangente de la curva, para ello tenemos que
 |
 |
 |
 |
de donde también
luego, la tangente unitaria a la curva en el punto (r,\theta) está dada por
de donde, el coseno del ángulo entre ésta tangente y la linea radial, es decir la dirección
,
está dado por 
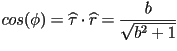
de donde, con un poco de trigonometría, obtenemos la misma expresión que antes.
Lo bueno del cálculo anterior es que también hemos obtenido el diferencial de la longitud de arco
,
con lo cual resulta de tan sólo una simple integración la
expresión de la longitud de arco:
y eso no es todo, como
ha sido encontrada en
función de 
, y como para un círculo de
radio 
, 
obtenemos que el radio de curvatura está dado por
y por ende, la curvatura
donde la curvatura está definida como el módulo del cambio del vector tangente con respecto al cambio de la longitud de arco, o también, como el cambio del angulo (con respecto a la horizontal) del vector tangente con respecto a la longitiud de arco, y como estamos tratando con una espiral equiangular este angulo es igual a
, de donde el resultado. Ojo que todas estas
definiciones de curvatura son equivalentes y sólo tratan de
formalizar lo que entendemos intuitivamente como el inverso
multiplicativo del radio de curvatura.La ecuación de Cesàro (i.e. la equación implicita que expresa la curva en terminos de su longitud de arco y su radio de curvatura [o equivalentemente su curvatura] ) está dada entonces por:
De este estudio, es fácil deducir que una espiral logarítmica se puede construir a partir de rayos igualmente espaciados comenzando en un punto a lo largo de un rayo, y dibujando el perpendicular a un rayo vecino. Cuando la distancia máxima angular entre un par arbitrario de radios es pequeña, la secuencia de segmentos se acerca al espiral logarítmico.
