|
   Curvas
de una Curva Plana. Curvas
de una Curva Plana.
Introducción
(nociones
básicas).
El esquema general donde trabajaremos es un plano donde se encuentra
una curva genérica 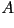 y un punto y un punto 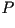 en en 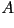 que se desplaza hasta
que se desplaza hasta 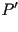 , en este contexto, dibujaremos
además las tangentes a la curva , en este contexto, dibujaremos
además las tangentes a la curva 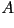 en los puntos en los puntos 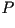 y
y 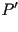 , y las llamaremos respectivamente , y las llamaremos respectivamente 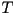 y y 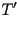 ,
al ángulo que se forma entre estas tangentes lo llamaremos ,
al ángulo que se forma entre estas tangentes lo llamaremos 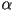 ,
también dibujaremos las normales a la curva ,
también dibujaremos las normales a la curva 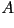 en los
puntos en los
puntos 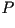 y y 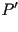 , y las llamaremos respectivamente , y las llamaremos respectivamente 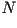 y
y 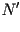 , todo lo anterior como se muestra en la siguiente figura , todo lo anterior como se muestra en la siguiente figura
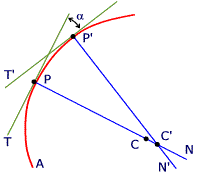
él cómo a través de una curva podemos obtener
estas tangentes y normales lo dejaremos de ejercicio, un método
es obtener la parametrización de la curva y luego hacer gala de
los conocimientos tanto de diferenciación como de
geometría analitica, conocimientos que no son necesarios para
entender las nociones básicas que a continuación
relataremos.
Observemos también, que el lector debe ser lo suficientemente
habil para entender la idea esencial, con la cual podrá explotar
su racionalidad y obtener la rigurosidad que desea.
Círculo
de Curvatura
La primera nocion básica es la de círculo de curvatura en
el punto 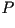 de la curva de la curva 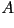 , y éste es el que
más se asemeja a la curva en el punto en cuestión, lo que
se puede apreciar en la siguiente figura , y éste es el que
más se asemeja a la curva en el punto en cuestión, lo que
se puede apreciar en la siguiente figura
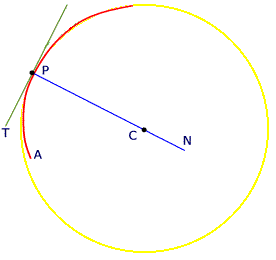
donde el círculo de curvatura de la curva 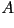 en el
punto en el
punto 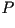 se ha dibujado en color amarillo. Notemos que
éste, también posee como tangente en el punto se ha dibujado en color amarillo. Notemos que
éste, también posee como tangente en el punto 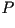 a
a 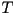 y que la normal a la curva y que la normal a la curva 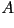 en el punto en el punto 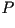 también pasa por su centro
también pasa por su centro 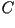 . En realidad la tangente
y la normal están estrechamente relacionadas con este
círculo. Este circulo se encuentra entonces totalmente
determinado por la tangente, la normal y su centro de circunferencia,
es por esto que en la primera figura sólo aparecen . En realidad la tangente
y la normal están estrechamente relacionadas con este
círculo. Este circulo se encuentra entonces totalmente
determinado por la tangente, la normal y su centro de circunferencia,
es por esto que en la primera figura sólo aparecen 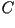 y y
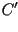 que son los centros de circunferencias de la curva que son los centros de circunferencias de la curva 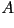 en los puntos
en los puntos 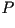 y y 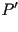 respectivamente respectivamente

recordemos que ésta es la figura con la que estamos trabajando.
Radio de
Curvatura
El radio de curvatura de la curva 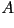 en el punto en el punto 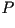 es el radio del círculo de curvatura. La noción es tan
sencilla, que plantear su definición de otra forma es
simplemente atrofiar la intuición. Además, por su misma
definición, resulta totalmente determinado el círculo de
curvatura sabiendo simplemente la normal a la curva en el punto y el
radio de curvatura. Recordemos también que la normal a la curva
se determina de forma directa con la tangente, como el producto cruz de
la tangente y un vector perpendicular al plano.
es el radio del círculo de curvatura. La noción es tan
sencilla, que plantear su definición de otra forma es
simplemente atrofiar la intuición. Además, por su misma
definición, resulta totalmente determinado el círculo de
curvatura sabiendo simplemente la normal a la curva en el punto y el
radio de curvatura. Recordemos también que la normal a la curva
se determina de forma directa con la tangente, como el producto cruz de
la tangente y un vector perpendicular al plano.
Observemos también que una recta tiene como círculo de
curvatura uno de radio infinito.
Curvatura
La curvatura se define como el inverso multiplicativo del radio de
curvatura, es decir, si 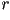 es el radio de curvatura de la
curva es el radio de curvatura de la
curva 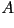 en el punto en el punto 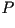 , la curvatura , la curvatura 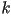 de
la curva de
la curva 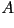 en el punto en el punto 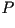 está dada por está dada por
por ejemplo una recta tentrá una curvatura 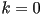 en todo punto.
en todo punto.
Obtención
práctica
Ahora bién, el lector que no sea completamente romo, se
habrá dado cuenta que encontrar el circulo de curvatura de una
curva arbitraria 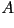 , es realmente un problema dificil con
estas definiciones, es más, resulta casi como una
aberración matemática el dibujar circulos una y otra vez
hasta dar con uno que se ajuste con nuestra curva. Es por esto que el
tener estas definiciones en la cabeza sin ocupar nuestra inteligencia
no nos sirven de nada, apliquemosla entonces. , es realmente un problema dificil con
estas definiciones, es más, resulta casi como una
aberración matemática el dibujar circulos una y otra vez
hasta dar con uno que se ajuste con nuestra curva. Es por esto que el
tener estas definiciones en la cabeza sin ocupar nuestra inteligencia
no nos sirven de nada, apliquemosla entonces.
Primero, recordamos que la suma de los ángulos internos de un
cuadrilátero es 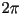 y entonces, como la suma de los
ángulos internos del cuadrilátero formado por las
tangentes y normales en los puntos y entonces, como la suma de los
ángulos internos del cuadrilátero formado por las
tangentes y normales en los puntos 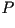 y y 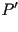 es es 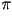 ,
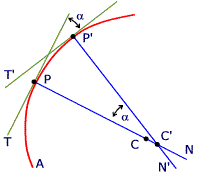
no queda otra que el ángulo entre las normales sea igual al
ángulo ,
no queda otra que el ángulo entre las normales sea igual al
ángulo 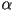 entre las tangentes, como se aprecia en
la siguiente figura entre las tangentes, como se aprecia en
la siguiente figura
Recordemos ahora que el ángulo 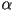 es muy facil de
determinar una vez que hemos obtenido las tangentes unitarias, pues su
coseno no es ni más ni menos que el producto punto entre ellas. es muy facil de
determinar una vez que hemos obtenido las tangentes unitarias, pues su
coseno no es ni más ni menos que el producto punto entre ellas.
Pues bien, la forma de determinar el radio de circunferencia en el
punto 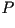 , es aproximandolo como el cociente entre la distancia
entre el punto , es aproximandolo como el cociente entre la distancia
entre el punto 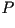 y el punto y el punto 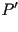 , que llamaremos , que llamaremos 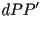 ,
y el ángulo ,
y el ángulo 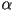 entre las tangentes de estos
puntos, es decir entre las tangentes de estos
puntos, es decir
esta ecuación, proviene del hecho, de que cuando 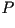 y y 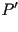 están muy próximos, los puntos
están muy próximos, los puntos 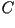 y y 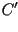 también lo estarán, y luego
también lo estarán, y luego 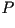 y y 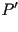 ,
aproximadamente formarán parte de un mismo circulo, claro
está que esta aproximación desaparece cuando el punto ,
aproximadamente formarán parte de un mismo circulo, claro
está que esta aproximación desaparece cuando el punto 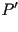 lo acercamos infinitesimalmente al punto
lo acercamos infinitesimalmente al punto 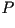 . .
  
|




 Curvas
de una Curva Plana.
Curvas
de una Curva Plana.