 |
Temas: Matemáticas. Naturaleza. Arte. Mapa del sitio. Mail. |
 |
Espirales
Arquimedeanas.
Introducción.
Una espiral arquimediana es una espiral cuya ecuación polar es de la forma:
,donde
es
la
distancia radial, 
es
el ángulo polar y 
es una
constante que determina cuan
enrollada está la espiral.Fue Sacchi (1854) quien distingió por primera vez este grupo de espirales.
Los valores de
correspondientes a una espiral con nombre particular están
resumidos en el siguiente cuadro:| espiral | |
| uniforme o de Arquimedes | 1 |
| hyperbolica | -1 |
| de Fermat | 2 |
| lituus | -2 |
Una espiral arquimedeana con parametro
tiene como inversa polar a una espiral
arquimedeana con parametro 
, de donde, se obtiene que la
espiral uniforme y la hiperbólica están inversamente
relacionadas, así como también la espiral de Fermat y el
lituus.La ecuación de Cesaró, la cual describe una curva en términos de su radio de curvartura y su longitud de arco, para una espiral arquimedeana es la siguiente:
La Curvatura de una espiral Arquimedeana está dada por:
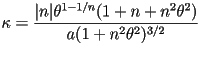
y la longitud de arco para
mayor estricto que 
está dada por:
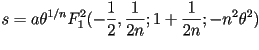,donde
es una función
hipergeométrica.
