 |
Temas: Matemáticas. Naturaleza. Arte. Mapa del sitio. Mail. |
 |
Matemáticas
de la Simetría espiral.
Introducción a las espirales
Cuando los fenómenos de rotación y expansión se unen dan lugar a una espiral.
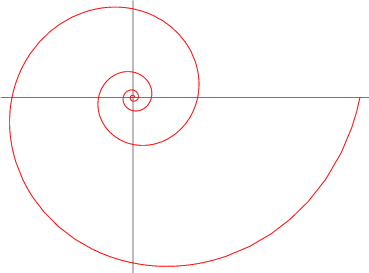
El concepto de espiral, ha encantado a los hombres, sobre todo a los matemáticos:
"La
espiral es un círculo espiritualizado. En la forma espiral, el
círculo, desenrollado, devanado, ha dejado de ser vicioso.La
vuelta sigue a la vuelta y toda síntesis es la tesis de una
nueva serie...." Vladimir
Nabokov.
"Había más imaginación en la cabeza de Arquímedes que en la de Homero" Voltaire.
Uno de los objetivos fundamentales de las Matemáticas a lo largo de la historia ha sido y continúa siendo interpretar el mundo que nos rodea.
"El
Universo
es un libro escrito en el
lenguaje de las matemáticas, siendo sus caracteres
triángulos, círculos y otras figuras geométricas,
sin las cuales es humanamente imposible comprender una sola palabra;
sin ellos sólo se conseguirá vagar por un obscuro
laberinto" Galileo
Galilei.
Mucho antes de que Galileo Galilei expresara de manera tan rotunda una de las funciones de las matemáticas, muchos sabios se habían puesto a la tarea de explicar los fenómenos naturales bajo la luz de la poderosa herramienta de las matemáticas.
Ante las innumerables manifestaciones naturales de las espirales, tanto de carácter orgánico como mecánico, estas curvas no podía dejar de llamar la atención de los matemáticos y ser objeto de su investigación. Sin embargo, como su propia forma sugiere, son curvas esquivas. No son curvas geométricas estáticas como la circunferencia, las cónicas o las lúnulas. Para construirlas se necesitan recursos mecánicos, algo que crece o que se mueve.
Pero, ¿qué es una espiral?, una definición formal sería la siguiente:
Se llama espiral a cualquier curva en el plano tal que la distancia
del origen a
todo punto de ella satisface la ecuación 
,donde
es una
función monótona y 
el
ángulo de
giro que se mide en
sentido contrario a las manecillas del reloj partiendo en el eje
horizontal (abscisa). Si esta definición la ampliamos al espacio obtendremos unas curvas espaciales parientes de las espirales llamadas hélices.
La historia de las espirales dentro del mundo matemático ha sido, paradógicamente una historia a saltos que trataremos de reproducir de una forma moderna y metódica.
