 |
Temas: Matemáticas. Naturaleza. Arte. Mapa del sitio. Mail. |
 |

2 Teoría de Grupos
2.1 Definiciones Básicas
Definición 5 (Grupo) Sea 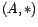 una estructura algebraica con una ley de
composición interna. Decimos que
una estructura algebraica con una ley de
composición interna. Decimos que 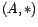 es un grupo si:
es un grupo si:
Con esta definición de grupo, es directo que el neutro es
único,
al igual que el inverso 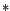 es asociativa.
es asociativa. 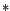 tiene neutro
tiene neutro 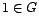 .
. - toda
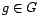 tiene inverso
tiene inverso
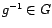 para
para 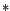 .
.
También se tienen las siguientes propiedades:
-
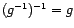 .
. -
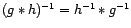 .
.
Ejemplos: Los siguientes son algunos ejemplos de grupos
-
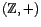 es un grupo abeliano.
es un grupo abeliano. 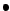
-
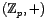 es un grupo abeliano.
es un grupo abeliano. 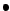
- Sea
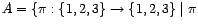 es
función biyectiva
es
función biyectiva 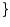 y se considera la
operación
y se considera la
operación 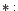 ``composición
de
funciones". Este conjunto tiene 6 elementos que se pueden nombrar
``composición
de
funciones". Este conjunto tiene 6 elementos que se pueden nombrar
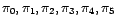 . Luego la
operación se puede ver en la tabla
Con esta operación
. Luego la
operación se puede ver en la tabla
Con esta operación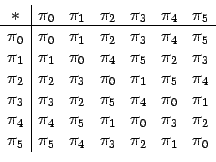
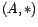 es un grupo, pero no
es abeliano.
es un grupo, pero no
es abeliano.
Definición 6 (Morfismo de grupos) Una
función 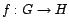 , entre dos grupos
, entre dos grupos
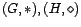 se dice morfismo
(u
homomorfismo) ssi:
se dice morfismo
(u
homomorfismo) ssi:
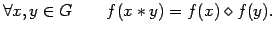
Un morfismo inyectivo suele llamarse monomorfismo, uno
sobreyectivo se llama epimorfismo, y finalmente un morfismo
biyectivo se llama isomorfismo.
Endomorfismo es un morfismo de un grupo en si mismo; un automorfismo es un isomorfismo endomorfo.
Propiedades
Si ![]() es un morfismo de grupos, entonces
es un morfismo de grupos, entonces
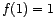 .
. - Si
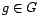 ,
,
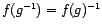 .
.
Con esto, ![]() es monomorfismo
es monomorfismo
![]() .
.
Ejemplos:
- La función logaritmo (en cualquier base),
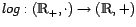 tiene la conocida
propiedad
tiene la conocida
propiedad 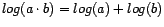 , y como es
biyectiva, es un
isomorfismo entre
, y como es
biyectiva, es un
isomorfismo entre
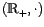 y
y 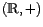 . Así
. Así
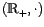 y
y 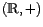 son estructuras isomorfas.
son estructuras isomorfas. 
- Si
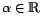 es un real fijo, la
función
es un real fijo, la
función
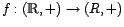 tal que
tal que
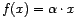 es un
homomorfismo, dado que
es un
homomorfismo, dado que
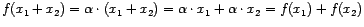 . Si además
. Si además
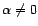 , entonces
, entonces 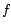 es un
automorfismo.
es un
automorfismo.
Definición 7 (Subgrupo) Si 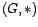 es un grupo, y
es un grupo, y
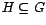 , diremos que
, diremos que 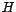 es un subgrupo
de
es un subgrupo
de 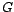 si
si 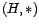 es
también un
grupo.
es
también un
grupo.
Si Una caracterización de los subgrupos es la siguiente:
![]() es subgrupo ssi:
es subgrupo ssi:
-
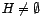 .
. -
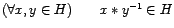 .
.
Definición 8 Si 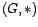 es
grupo, una relación de equivalencia
es
grupo, una relación de equivalencia 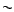 en G
se dice compatible con
en G
se dice compatible con 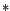 ssi:
ssi:
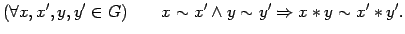
Dada una relación de equivalencia ![]() compatible con
compatible con ![]() ,
podemos definir una l.c.i. en el conjunto cociente
,
podemos definir una l.c.i. en el conjunto cociente ![]() .
.
| |
Ahora, si ![]() es compatible con
es compatible con ![]() , entonces
, entonces
Llamemos
Si ![]() y
y ![]() es
un elemento
cualquiera de
es
un elemento
cualquiera de ![]() , entonces
, entonces
![]() .
En efecto:
.
En efecto:
O sea,
Definición 9 (Subgrupo normal) Un
subgrupo H de G tal que satisface
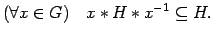 se llama subgrupo normal de G.
se llama subgrupo normal de G.
Se usará la siguiente notación para designar a los
subgrupos
normales de  es de equivalencia en G.
es de equivalencia en G.  es compatible con
es compatible con  .
. ![$ [1] = H$](imagenes/img294.png) .
.
- Cualquier subgrupo de un grupo Abeliano
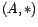 es un subgrupo normal, gracias a la
conmutatividad de
la operación
es un subgrupo normal, gracias a la
conmutatividad de
la operación 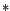 . En efecto, sea
. En efecto, sea 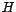 subgrupo de
subgrupo de 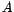 . Entonces
. Entonces
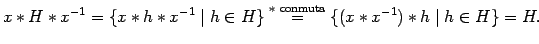
- El núcleo de todo morfismo de
grupos
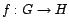 es un subgrupo normal de G; es
más, todos los
subgrupos normales de G son núcleos de algún morfismo. En
efecto
es un subgrupo normal de G; es
más, todos los
subgrupos normales de G son núcleos de algún morfismo. En
efecto
- Si
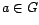 y
y
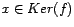 Por lo tanto
Por lo tanto
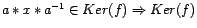 subgrupo normal.
subgrupo normal. - Si
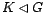 , tomemos
, tomemos 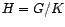 y
y
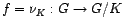 morfismo. Luego
Luego
morfismo. Luego
Luego![$\displaystyle \nu_{K}(x) = 1 \in G/K \Leftrightarrow [x] = [1] = K \Leftrightarrow x \in K.$](imagenes/img304.png)
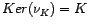 .
.
- Si
Definición 10 (Subgrupo generado por un subconjunto)
Sea 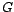 un grupo, y
un grupo, y
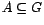 un subconjunto cualquiera.
Denotemos
un subconjunto cualquiera.
Denotemos
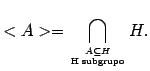 el subgrupo generado por A.
el subgrupo generado por A.
Se tiene 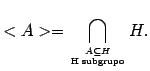
Es también claro que
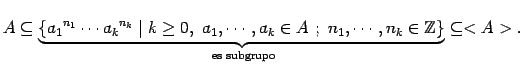
Caso interesante
Si ![]() entonces
entonces ![]() y se
denomina subgrupo cíclico generado por a.
y se
denomina subgrupo cíclico generado por a.
Un grupo ![]() se dice cíclico si
se dice cíclico si
Teorema 1 (Teorema del factor) Si 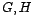 grupos,
grupos, 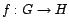 morfismo, y
morfismo, y 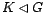 tal que
tal que
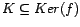 . Entonces:
. Entonces:
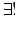 morfismo
morfismo 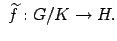 tal que el diagrama siguiente es conmutativo
tal que el diagrama siguiente es conmutativo
![$\displaystyle \xymatrix{G \ar[rr]^f \ar[dr]^{\nu} & & H \\
& G/H \ar[ur]^{\widetilde{f}} & }
$](imagenes/img322.png) Con
Con 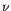 el epimorfismo canónico
(introducido
anteriormente). Es
claro que
el epimorfismo canónico
(introducido
anteriormente). Es
claro que 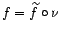 . Se dice que f se
factoriza a través de G/K. Además
. Se dice que f se
factoriza a través de G/K. Además
Usando este resultado se puede demostrar la siguiente
proposición
![$\displaystyle \xymatrix{G \ar[rr]^f \ar[dr]^{\nu} & & H \\
& G/H \ar[ur]^{\widetilde{f}} & }
$](imagenes/img322.png)
| f es un epimorfismo | |
|
| |
|
|
Proposición 2 Si G es un grupo
cíclico, entonces:
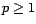 ( notemos que
( notemos que 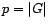 ).
).
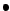
- Si G es infinito
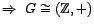 .
. 
- Si G es finito
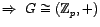 .
.




