 |
Temas: Matemáticas. Naturaleza. Arte. Mapa del sitio. Mail. |
 |

3 Acciones de Grupos
Definición 11 Sea 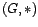 un
grupo, y
un
grupo, y  un conjunto. Una acción (izq) de
un conjunto. Una acción (izq) de 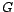 en
en 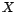 es una función
es una función
Con las siguientes propiedades
Ahora veamos algunos ejemplos de acciones:
| |
|
|
|
| |
|
|
- Sea
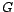 un grupo cualquiera de
un grupo cualquiera de
 , donde
, donde
 es biyectiva
es biyectiva . La siguiente
es una acción de
. La siguiente
es una acción de 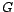 en
en 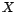 :
:

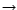
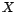

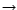
 .
. - Sea
 . La siguiente es una acción de
. La siguiente es una acción de 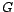 (como grupo) en
(como grupo) en 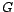 (como conjunto).
(como conjunto).

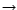
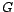

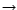
 .
. - Acción de
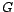 sobre si mismo por
conjugación
sobre si mismo por
conjugación

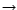
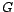

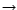
 .
.
| |
|||
|
|
|
|
Si
|
|
| |
Al reves, si
| |
|||
|
|

Una acción se dice transitiva si produce una sola órbita, es decir ssi:
Si ![]() es un grupo, y
es un grupo, y ![]() son dos
son dos
![]() -espacios. Un
morfismo de G-espacios es una función
-espacios. Un
morfismo de G-espacios es una función ![]() tal que :
tal que :
Sea ![]() un
un ![]() -espacio, y sea
-espacio, y sea
![]() . Se denotara estabilizador
de
. Se denotara estabilizador
de ![]() al subconjunto de
al subconjunto de ![]() :
:
Teorema 2 Si 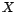 es un
es un 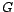 -espacio homogéneo, entonces
-espacio homogéneo, entonces
 isomorfismo de G-espacios
isomorfismo de G-espacios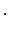 donde
donde  ,
,
 cualquiera.
cualquiera.




