 |
Temas: Matemáticas. Naturaleza. Arte. Mapa del sitio. Mail. |
 |


1 Preliminares.
Subsecciones- 1.1 Relaciones.
- 1.2
Relaciones donde
 .
. - 1.3 Relaciones de equivalencia.
- Estructuras Algebraicas
- 1.4 Leyes de composición interna
- 1.5 Propiedades básicas de las l.c.i
1.1 Relaciones.
Ejemplos:
-
 , donde
, donde

(congruencia módulo 3). -
 ,
donde
,
donde
 (divisibilidad en
(divisibilidad en
 ).
). -
 , donde
, donde
 .
.
Toda función induce a una relación. Si ![]() es una función,
la relación asociada es
es una función,
la relación asociada es
![]() , donde
el conjunto de pares ordenados
, donde
el conjunto de pares ordenados ![]() está dado por
está dado por
Igualdad de relaciones: De la definición de
relación como
una terna, es directo que dos relaciones
![]() y
y ![]() son
iguales ssi
son
iguales ssi
![]() . A
su vez, es también claro que si
. A
su vez, es también claro que si
![]() ,
entonces
,
entonces
![]() De aquí que
se cumple:
De aquí que
se cumple:
-
 y
y  tienen el mismo conjunto de
partida
tienen el mismo conjunto de
partida 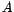 ,
, -
 y
y  tienen el mismo
conjunto de llegada
tienen el mismo
conjunto de llegada  , y
, y - Los elementos se relacionan por
 y
y  de la misma forma, es decir,
de la misma forma, es decir,
1.2 Relaciones donde  .
.
Sea A un conjunto no vacío. Llamaremos a una relación
- Reflexividad: Decimos que
 es refleja
(o reflexiva) ssi
es refleja
(o reflexiva) ssi
 .
. - Simetría: Decimos que
 es simétrica ssi
es simétrica ssi
 .
. - Antisimetría: Decimos que
 es antisimétrica
ssi
es antisimétrica
ssi
 .
. - Transitividad: Decimos que
 es transitiva ssi
es transitiva ssi
 .
.
Ejemplo importante:
Estudiemos las 4 propiedades
anteriores para la relación ![]() en
en ![]() tal que
tal que
- Simetría: Sean
 tales que
tales que  . Hay que probar que
. Hay que probar que
 . Sabemos que
. Sabemos que
 . Sea
. Sea
 tal que
tal que  . Despejando se tiene
que
. Despejando se tiene
que  , Es decir hemos encontrado un
entero
, Es decir hemos encontrado un
entero  tal que
tal que  lo que
prueba que
lo que
prueba que  .
. 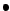
- Refleja: Sea
 . Debemos probar que
. Debemos probar que
 . Es decir hay que
encontrar
. Es decir hay que
encontrar  tal que
tal que  . Basta tomar
. Basta tomar  , con lo cual
, con lo cual
 y se concluye que
y se concluye que
 .
. 
- Transitividad: Sean
 tales que
tales que  . Hay que probar
que
. Hay que probar
que  . Se tiene
. Se tiene
 para un cierto
para un cierto
 , y
, y
 para un cierto
para un cierto
 . Luego,
despejando, se obtiene
. Luego,
despejando, se obtiene
 . Hemos
encontrado un entero
. Hemos
encontrado un entero  tal que
tal que
 , luego
, luego
 .
. 
- Antisimetría:
No lo es si
 pues, por ejemplo si
pues, por ejemplo si  , se tiene
que
, se tiene
que  y además
y además  pero
pero  . Si
. Si  , la relación
, la relación  es la igualdad en
es la igualdad en
 , por lo que
no es sorprendente que
, por lo que
no es sorprendente que  sea también antisimétrica.
sea también antisimétrica.
- (a)
-
 .
. - (b)
-
 .
.
- (a)
- Sumando estas ecuaciones, obtenemos
 , de donde sale que
, de donde sale que
 .
. - (b)
- Multiplicando las mismas ecuaciones, obtenemos
 , de donde sale que
, de donde sale que
 .
.
- Decimos que una relación
 en
en 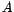 es de equivalencia
ssi es refleja, simétrica y transitiva.
es de equivalencia
ssi es refleja, simétrica y transitiva. - Decimos que una relación
 en
en 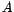 es de orden
ssi es refleja, antisimétrica y transitiva.
es de orden
ssi es refleja, antisimétrica y transitiva.
Si
 es una relación de orden en
es una relación de orden en 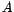 , entonces si
, entonces si
 decimos que
decimos que  precede de
precede de  , y diremos que
, y diremos que  y
y  son comparables ssi
son comparables ssi
 . Distinguimos
dos tipos de ordenes:
. Distinguimos
dos tipos de ordenes: - (a)
- Orden parcial: Si existe al menos un par de
elementos
 que no son comparables por
que no son comparables por
 .
. - (b)
- Orden total: Si todo par de elementos
 son
comparables por
son
comparables por  .
.
1.3 Relaciones de equivalencia.
Recordemos que una relación ![]() en
en ![]() es de equivalencia
ssi es
refleja, simétrica y transitiva.
es de equivalencia
ssi es
refleja, simétrica y transitiva.
- Para cada
![$ a \in A, \ [a]_{\mathcal{R}} \neq \emptyset$](imagenes/img111.png) .
. - Para
cada par de elementos
 , si
, si
 , entonces
, entonces
![$ [a]_{\mathcal{R}} = [b]_{\mathcal{R}}$](imagenes/img112.png) .
. - Para cada par de elementos
 ,
si
,
si  , entonces
, entonces
![$ [a]_{\mathcal{R}} \cap [b]_{\mathcal{R}} =
\emptyset$](imagenes/img113.png) .
.
Las dos propiedades anteriores permiten definir una
partición de ![]() .
.
Esto es, una familia de subconjuntos de ![]() , dos a
dos disjuntos,
cuya unión es
, dos a
dos disjuntos,
cuya unión es ![]() . De manera más precisa,
existe un conjunto de
subconjuntos no vacíos de
. De manera más precisa,
existe un conjunto de
subconjuntos no vacíos de ![]() ,
,
![]() (que
será la partición de
(que
será la partición de ![]() ), tal que si
), tal que si
![]() entonces
entonces
![]() (dos a dos disjuntos) y
(dos a dos disjuntos) y


La partición que nos interesa construir es la formada por las
clases de equivalencia de ![]() , es decir,
, es decir,
Ejemplo importante:
Para ![]() , encontrar el conjunto cociente de
, encontrar el conjunto cociente de
![]() por la
relación de equivalencia
por la
relación de equivalencia ![]() , que denotamos por
, que denotamos por
![]() (los ``enteros módulo p"). Denotamos a
la clase de equivalencia
de
(los ``enteros módulo p"). Denotamos a
la clase de equivalencia
de
![]() como
como ![]() . Veamos primero un par de casos
triviales:
. Veamos primero un par de casos
triviales:
- Si
 , sabemos que
, sabemos que  es la
igualdad en
es la
igualdad en  ,
y entonces
,
y entonces ![$ [n]_{0} = \{ n \}$](imagenes/img124.png) para cada
para cada  . Luego
. Luego
 .
. 
- Si
 , entonces es directo que
, entonces es directo que
 , por lo que hay una sola clase de
equivalencia:
, por lo que hay una sola clase de
equivalencia:
![$ [n]_{1} = \mathbbm{Z}$](imagenes/img128.png) para todos los enteros
para todos los enteros  , y
, y
 (un conjunto con un solo elemento).
(un conjunto con un solo elemento).
Ahora supondremos que ![]() . Esta es la
restricción que
generalmente se impone cuando se usan las congruencias módulo
. Esta es la
restricción que
generalmente se impone cuando se usan las congruencias módulo ![]() en la práctica. Haremos uso de la división de
números enteros, que
se puede enunciar como sigue: Si
en la práctica. Haremos uso de la división de
números enteros, que
se puede enunciar como sigue: Si
![]() y
y ![]() ,
entonces existe una única pareja de enteros
,
entonces existe una única pareja de enteros ![]() , llamados
respectivamente cociente y resto de la división de
, llamados
respectivamente cociente y resto de la división de ![]() por
por ![]() ,
tales que
,
tales que ![]() , y además
, y además ![]() .
.
Si ![]() es un entero cualquiera, dividiéndolo por
es un entero cualquiera, dividiéndolo por ![]() obtenemos
obtenemos ![]() , con
, con ![]() .
Pero esta
ecuación dice que
.
Pero esta
ecuación dice que ![]() , es decir, que
, es decir, que
![]() . De aquí que las clases de equivalencia
para
. De aquí que las clases de equivalencia
para ![]() son sólo
son sólo ![]() . Además
estas
. Además
estas ![]() clases son distintas entre sí, puesto que si
clases son distintas entre sí, puesto que si
![]() ,
para
,
para ![]() , entonces
, entonces ![]() . Pero como también
. Pero como también
![]() , entonces la
unicidad de la división de
, entonces la
unicidad de la división de ![]() por
por ![]() entrega
entrega ![]() .
.
Concluimos entonces que
![]() , y tiene
exactamente
, y tiene
exactamente ![]() elementos.
elementos.
Estructuras Algebraicas
1.4 Leyes de composición interna
- En
 definimos la ley de composición interna suma módulo 2
por la siguiente tabla
(se lee por ejemplo
definimos la ley de composición interna suma módulo 2
por la siguiente tabla
(se lee por ejemplo
 ). También se define la multiplicación
modulo 2 por
). También se define la multiplicación
modulo 2 por

- En
 definimos la ley de composición interna suma
módulo 4 por la siguiente tabla
definimos la ley de composición interna suma
módulo 4 por la siguiente tabla

- El conjunto
 tiene la operación de suma como
l.c.i.
tiene la operación de suma como
l.c.i. - El conjunto
 de los numeros reales tiene a la
suma como l.c.i.
de los numeros reales tiene a la
suma como l.c.i. - Generalizando los ejemplos 1 y 2, para cada
 con
con  , definiremos una suma y una
multiplicación en el conjunto
, definiremos una suma y una
multiplicación en el conjunto
 de los enteros módulo
de los enteros módulo  .
Recordemos de los ejemplos importantes anteriores que
.
Recordemos de los ejemplos importantes anteriores que
 es
el conjunto cociente de los enteros
es
el conjunto cociente de los enteros  por la relación
por la relación
 de congruencia
módulo
de congruencia
módulo  , y que
, y que
![$ \mathbbm{Z}_{p} = \big\{ [0]_{p},[1]_{p}, ... ,
[p-1]_{p} \big\} $](imagenes/img147.png) . También
vimos que
. También
vimos que
 cumplía las
siguientes propiedades:
cumplía las
siguientes propiedades:
 . Esto se
puede reescribir como
(Hemos omitido el subíndice
. Esto se
puede reescribir como
(Hemos omitido el subíndice![$\displaystyle (\forall m_{1},m_{2},n_{1},n_{2} \in \mathbbm{Z}) \
[m_{1}] = [m...
...m_{1}+m_{2}]=[n_{1}
+ n_{2}] \wedge [m_{1} \cdot m_{2}] = [n_{1} \cdot n_{2}].$](imagenes/img163.png)
 de la
notación de las clases de
equivalencia para facilitar un poco la lectura). Esta última
propiedad nos indica que no hay ninguna ambigüedad al definir,
para
de la
notación de las clases de
equivalencia para facilitar un poco la lectura). Esta última
propiedad nos indica que no hay ninguna ambigüedad al definir,
para
![$ [m],[n] \in \mathbbm{Z}_{p},\ [m] +_{p} [n] = [m+n] \in \mathbbm{Z}_{p}, \
[m] \cdot [n] = [m \cdot n] \in \mathbbm{Z}_{p}$](imagenes/img164.png) (ya que,
módulo
(ya que,
módulo  , las
operaciones no dependen del representante de cada clase). Resulta
entonces que tenemos dos leyes de composición interna,
, las
operaciones no dependen del representante de cada clase). Resulta
entonces que tenemos dos leyes de composición interna,  y
y  , definidas sobre
, definidas sobre
 .
.
Para simplificar la notación, muchas veces se eliminan incluso los paréntesis de la notación de clases de equivalencia en
 ,
escribiendo
,
escribiendo  . Suele
también denotarse el
+ de
. Suele
también denotarse el
+ de  como
como  y el
y el  de
de
 como
como  .
Con estas convenciones, el ejemplo 1 es
simplemente
la suma y el producto en
.
Con estas convenciones, el ejemplo 1 es
simplemente
la suma y el producto en  , y el ejemplo 2 corresponde a la
suma en
, y el ejemplo 2 corresponde a la
suma en  .
.
1.5 Propiedades básicas de las l.c.i
Sea- Elementos Neutros: Decimos que
 es un
elemento
neutro para una ley de composición interna
es un
elemento
neutro para una ley de composición interna 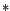 si se
cumple
Propiedad: El neutro, cuando existe, es único (y tenemos entonces derecho a hablar de el neutro).
si se
cumple
Propiedad: El neutro, cuando existe, es único (y tenemos entonces derecho a hablar de el neutro).
En efecto, supongamos que existen neutros
 y
y  . Luego
. Luego  .
. - Asociatividad: Decimos que la
l.c.i. en
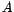 es asociativa ssi
es asociativa ssi

- Elementos inversos: Si existe neutro
 , decimos
que
, decimos
que  tiene a
tiene a  como inverso, o que
como inverso, o que  es un
inverso para
es un
inverso para  ssi
En general, un inverso
ssi
En general, un inverso
 para
para  no es único.
Cuando sea único lo
denotaremos
no es único.
Cuando sea único lo
denotaremos  . Una condición de unicidad
es la siguiente,
. Una condición de unicidad
es la siguiente,
Propiedad: Si
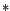 tiene neutro y es
asociativa
entonces los inversos son únicos.
tiene neutro y es
asociativa
entonces los inversos son únicos. En efecto, sean
 tales que
tales que
 y
y
 .
Luego operando por
.
Luego operando por  la primera igualdad por la
izquierda se
obtiene
la primera igualdad por la
izquierda se
obtiene  . Como la ley
es asociativa entonces
. Como la ley
es asociativa entonces
 , de lo
que deducimos que
, de lo
que deducimos que  .
. - Conmutatividad: Decimos que la l.c.i.
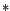 en
en 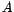 es conmutativa ssi
es conmutativa ssi

Supongamos que ![]() es una estructura algebraica
asociativa
y con neutro
es una estructura algebraica
asociativa
y con neutro ![]()
- Si
 tiene inverso que llamamos
tiene inverso que llamamos  entonces
entonces  tiene inverso y es
tiene inverso y es
 . En efecto,
buscamos
. En efecto,
buscamos  tal que
tal que
 .
Pero sabemos que
.
Pero sabemos que  , luego por
unicidad
, luego por
unicidad  .
. - Si
 tiene inverso
tiene inverso  y
y  tiene inverso
tiene inverso  entonces
entonces  tiene inverso y
es
tiene inverso y
es 
Verifiquemos que
 Por unicidad,
Por unicidad,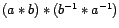
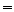
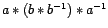
(asociatividad) 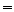
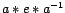
(  inverso de
inverso de  )
)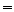
 ,
,(razones similares) 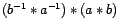
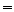
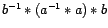
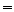
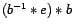
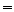
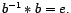
 es el inverso.
es el inverso.
Veamos algunas propiedades adicionales de las l.c.i.:
- Cancelabilidad: Un elemento
 es cancelable
ssi
Algunos elementos cancelables: Si existe neutro
es cancelable
ssi
Algunos elementos cancelables: Si existe neutro
 , este es
cancelable; si existe neutro
, este es
cancelable; si existe neutro  y la l.c.i. es
asociativa,
entonces si
y la l.c.i. es
asociativa,
entonces si  tiene inverso, será cancelable. En
efecto
tiene inverso, será cancelable. En
efecto
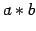
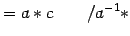
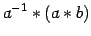
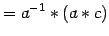
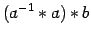
 (asociatividad)
(asociatividad)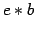
 inverso de
inverso de 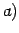
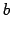
 neutro
neutro
Análogamente se prueba que si
si  es invertible.
es invertible. - Elemento Absorbente (cero):
 es
un elemento absorbente ssi
Por ejemplo en
es
un elemento absorbente ssi
Por ejemplo en
 el 0 es absorbente.
el 0 es absorbente. - Elemento Idempotente:
 es
un elemento idempotente ssi
es
un elemento idempotente ssi  . A modo de
ejemplo, un neutro y un absorbente son siempre idempotentes.
. A modo de
ejemplo, un neutro y un absorbente son siempre idempotentes.





