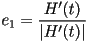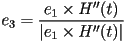|
   Construcción
de caracolas. Construcción
de caracolas.
Incorporando
la curva generadora al modelo.
La curva generatriz 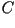 se especifica
en un sistema de coordenadas locales se especifica
en un sistema de coordenadas locales 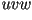 . Dado un
punto . Dado un
punto 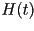 de
la
hélico-espiral de
la
hélico-espiral 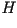 , primero se pondera , primero se pondera 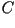 por
el factor por
el factor 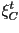 con respecto al origen
con respecto al origen 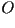 de este sistema, luego se rota y
traslada hasta que el origen de este sistema, luego se rota y
traslada hasta que el origen 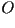 de la curva coincida con de la curva coincida con 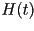 como se muestra en la figura:
como se muestra en la figura:
A
continuación los ejes 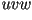 son usados
para orientar la curva generadora en el espacio son usados
para orientar la curva generadora en el espacio
La
solución simple
La solución
más simple
es rotar el sistema 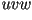 hasta que el eje hasta que el eje 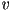 sea
paralelo al eje sea
paralelo al eje 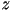 y el eje y el eje 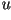 sea perpendicular al
eje sea perpendicular al
eje 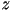 . .
En este caso, si la curva generadora yace en
el plano 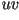 , la abertura de la concha y las marcas de
crecimiento (tales como el relieve en la superficie de la caracola)
serán
paralelas al eje de la concha. Sin embargo, muchas conchas exhiben
aproximadamente marcas de crecimiento ortoclinales las que yacen en
planos normales a la hélico-espiral , la abertura de la concha y las marcas de
crecimiento (tales como el relieve en la superficie de la caracola)
serán
paralelas al eje de la concha. Sin embargo, muchas conchas exhiben
aproximadamente marcas de crecimiento ortoclinales las que yacen en
planos normales a la hélico-espiral  . La diferencia
entre este modelo y una verdadera caracola se puede apreciar en la
siguiente figura: . La diferencia
entre este modelo y una verdadera caracola se puede apreciar en la
siguiente figura:
Una
solución más sofisticada
Una mejor solución, que captura este efecto, se obtiene
orientado el eje 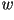 a lo largo del
vector
a lo largo del
vector 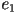 , tangente a la hélico-espiral en el punto , tangente a la hélico-espiral en el punto 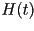 .
La curva se
fija en el espacio alineando el eje .
La curva se
fija en el espacio alineando el eje 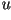 con el vector normal
principal con el vector normal
principal 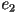 de
de 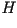 . Los vectores unitarios . Los vectores unitarios 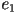 y y 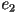 se pueden obtener con las siguientes fórmulas:
se pueden obtener con las siguientes fórmulas:
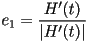 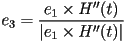
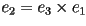
Donde 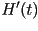 y y 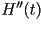 denotan a la primera y segunda derivada del vector posición
denotan a la primera y segunda derivada del vector posición 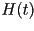 ,
tomada con respecto a ,
tomada con respecto a 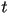 . Los vectores . Los vectores 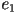 , , 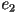 y
y 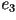 definen un sistema local de coordenadas ortonormales
llamado triedro de Frenet.
Éste, es considerado un
buen sistema de referencia para orientaciones más sofisticadas,
ya que no
depende de la parametrización de la hélico-espiral definen un sistema local de coordenadas ortonormales
llamado triedro de Frenet.
Éste, es considerado un
buen sistema de referencia para orientaciones más sofisticadas,
ya que no
depende de la parametrización de la hélico-espiral 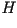 o del
sistema de
coordenadas en la que es expresado. El triedro de Frenet no está
definido en los puntos sin curvatura, sin embargo, una
hélico-espiral siempre tiene curvatura no nula (
o del
sistema de
coordenadas en la que es expresado. El triedro de Frenet no está
definido en los puntos sin curvatura, sin embargo, una
hélico-espiral siempre tiene curvatura no nula (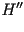 nunca se anula). El impacto en la orientación de la curva
generadora se puede apreciar en la siguiente figura:
nunca se anula). El impacto en la orientación de la curva
generadora se puede apreciar en la siguiente figura:
donde se verifica que la abertura, así como el relieve, de la
caracola real (ubicada a la izquierda), se ajusta mucho mejor al modelo
que usa el triedro de Frenet (ubicado en el centro) en la
orientación de la curva generadora, también se puede
apreciar que el modelo más simple está lejos de ser el
más adecuado.
En
general la curva no se encuentra alineada ni con el eje de la caracola
ni con
el triedro de Frenet. Es más, en el caso de curvas que no sean
planas es difícil
definir lo que es estar alineado. También, resulta conveniente
poder ajustar la
orientación de la curva generadora con respecto a las
coordenadas del sistema de referncia. Con este objetivo, nosotros
permitimos la rotacion del sistema 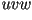 con respecto
a cada eje con respecto
a cada eje 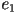 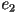 y y 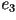 . .
  
|




 Construcción
de caracolas.
Construcción
de caracolas.
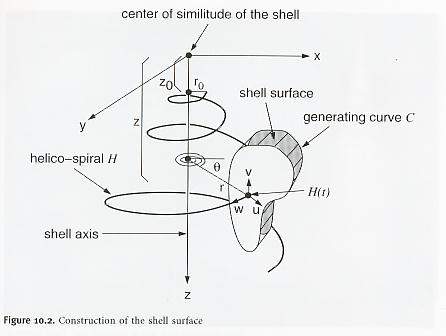
 son usados
para orientar la curva generadora en el espacio
son usados
para orientar la curva generadora en el espacio