|
   Construcción
de caracolas. Construcción
de caracolas.
Construcción
de la malla poligonal.
En el sentido matemático, la superficie de la caracola se define
completamente con la curva generadora 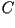 , barriendola a lo
largo de la hélico-espiral , barriendola a lo
largo de la hélico-espiral 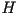 Sin embargo, nosotros
representaremos esta superficie como una malla poligonal con el
propósito de renderizarla. La malla se construye especificando Sin embargo, nosotros
representaremos esta superficie como una malla poligonal con el
propósito de renderizarla. La malla se construye especificando 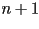 puntos en la curva generadora (incluyendo los puntos finales), y luego
conectandolos con sus correspondientes puntos de la siguiente curva
generadoora. La secuencia de poligonos que se encuentran en un par de
curvas generadoras adyacentes se llama rim.
puntos en la curva generadora (incluyendo los puntos finales), y luego
conectandolos con sus correspondientes puntos de la siguiente curva
generadoora. La secuencia de poligonos que se encuentran en un par de
curvas generadoras adyacentes se llama rim.
Al igual que en el proceso de orientación de la curva
generadora, la obtención del rim cuenta con
al menos dos formas posibles de llevarse a cabo
La
solución simple
Sea 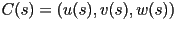 una parametrización de la
curva generadora una parametrización de la
curva generadora 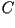 en las coordenadas en las coordenadas 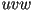 , con , con 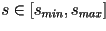 . .
La forma más sencilla, es particionar 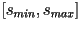 uniformemente en
uniformemente en 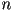 intervalos de largo intervalos de largo 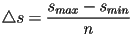 , y luego obtener los , y luego obtener los 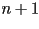 puntos en la curva generadora como los valores de
puntos en la curva generadora como los valores de 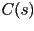 en los
extremos de estos intervalos. en los
extremos de estos intervalos.
El problema con ésta solución es, que la distancia
geodesica de los puntos en la curva generadora dependerá de la
velocidad con que es hecha la parametrización de la curva, lo
que trae problemas al tratar de modelar fenómenos como el
relieve o la textura de la superficie de la caracola.
Una
solución más sofisticada
Sea nuevamente 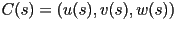 una
parametrización de la
curva generadora una
parametrización de la
curva generadora 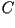 en las coordenadas en las coordenadas 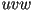 , con , con 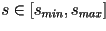 . .
Una forma más sofisticada, es particionar, esta vez la curva 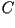 uniformemente en intervalos de largo
uniformemente en intervalos de largo 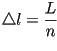 ,
donde ,
donde 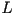 denota al largo de la curva denota al largo de la curva 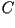 . Ésta
es una mejor solución al tratar de modelar fenómenos como
el relieve o la textura de la superficie. La diferencia entre
ésta forma y la anterior solución se puede apreciar en la
siguiente figura: . Ésta
es una mejor solución al tratar de modelar fenómenos como
el relieve o la textura de la superficie. La diferencia entre
ésta forma y la anterior solución se puede apreciar en la
siguiente figura:
El método, es muy sencillo; dado que el largo de un arco
infinitesimal 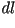 en en 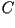 se relaciona con el cambio
infinitesimal se relaciona con el cambio
infinitesimal 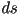 del parametro del parametro 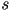 por medio de las
siguientes ecuaciones: por medio de las
siguientes ecuaciones:
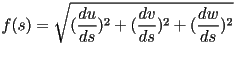 .
El largo total 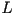 de de 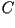 se puede obtener integrando se puede obtener integrando 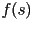 sobre el intervalo
sobre el intervalo 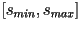 : :
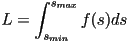 .
Invirtiendo la primera ecuación, obtenemos que:
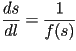 .
Que junto con la condición inicial 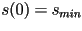 , forma
una ecuación diferencial de primer orden que determina al
parametro , forma
una ecuación diferencial de primer orden que determina al
parametro 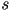 como función del largo del arco como función del largo del arco 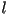 .
Luego, integrando esta última ecuación en .
Luego, integrando esta última ecuación en 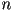 intervalos consecutivos de largo
intervalos consecutivos de largo 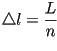 ,
obtenemos una secuencia de ,
obtenemos una secuencia de 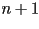 valores de parametros: valores de parametros:
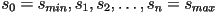 ,
con los cuales se obtiene la secuencia de 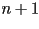 puntos en la
curva generadora que poseen la propiedad buscada. puntos en la
curva generadora que poseen la propiedad buscada.
  
|




 Construcción
de caracolas.
Construcción
de caracolas.
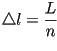 ,
donde
,
donde 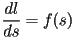
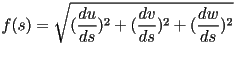 .
.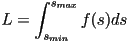 .
.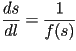 .
.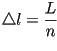 ,
obtenemos una secuencia de
,
obtenemos una secuencia de 






