|
   Construcción
de caracolas. Construcción
de caracolas.
La
hélico espiral.
Han habido numerosos adelantos en el modelamiento de las caracolas
desde los primeros trabajos de Raup. En los métodos modernos, el
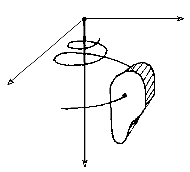
modelamiento de la superficie de la caracola comienza con la
construcción de una hélico-espiral logarítmica
(equiangular) 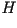 . .
Recordemos que en un sistema de coordenadas cilíndricas esta se
describe de la siguiente forma:
El parámetro 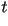 , el tiempo, empieza de , el tiempo, empieza de 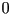 en
el
vértice de la caracola y termina en en
el
vértice de la caracola y termina en 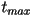 con su
abertura. Las primeras dos ecuaciones representan un espiral
logarítmico en el plano con su
abertura. Las primeras dos ecuaciones representan un espiral
logarítmico en el plano 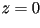 . La tercera ecuación propaga el espiral a lo largo de eje z,
esto contribuye con la componente helicoidal
de la forma de la caracola.
. La tercera ecuación propaga el espiral a lo largo de eje z,
esto contribuye con la componente helicoidal
de la forma de la caracola.
Las distancias 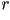 y y 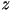 son funciones exponenciales
del parámetro son funciones exponenciales
del parámetro 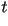 , y
usualmente tienen la misma base: , y
usualmente tienen la misma base:
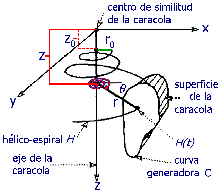
Debido a la construcción, la hélico-espiral generada es
similar a
sí misma, con centro de similitud localizado en el origen del
sistema de coordenadas. Dados los valores iniciales 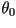 , ,
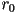 , y , y 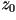 , una secuencia de puntos en el
hélico-espiral puede ser obtenida usando las siguientes
fórmulas: , una secuencia de puntos en el
hélico-espiral puede ser obtenida usando las siguientes
fórmulas:
Mientras el ángulo de rotación 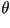 se
incrementa en progresión aritmética con paso se
incrementa en progresión aritmética con paso 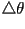 ,
el radio ,
el radio 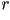 forma una progresión geométrica con
factor de escalamiento: forma una progresión geométrica con
factor de escalamiento:
y el desplazamiento vertical 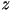 forma una progresión
geométrica con factor de escalamiento: forma una progresión
geométrica con factor de escalamiento:
En muchas caracolas, se tiene que 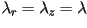 .
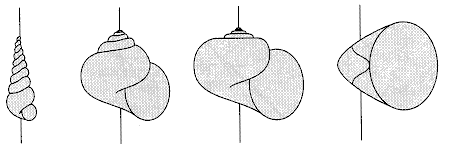
En la siguiente figura se muestran algunos de estos ejemplos, cuya
diferencia radica en los diferentes parámetros del
hélico-espiral. .
En la siguiente figura se muestran algunos de estos ejemplos, cuya
diferencia radica en los diferentes parámetros del
hélico-espiral.
 |
Turbinate
shell (leftmost) z0=1.9, λ=1.007
Patelliform shell (top left) z0=0, λ=1.34
Spherical shell (bottom left) z0=1.5, λ=1.03
Tubular shell (top right) z0=0, λ=1.011
Diskoid shell (bottom right) z0=1.4, λ=1.014 |
  
|




 Construcción
de caracolas.
Construcción
de caracolas.