 |
Temas: Matemáticas. Naturaleza. Arte. Mapa del sitio. Mail. |
 |
La
proporción áurea o "el número de oro" 
.
La trigonometría y el número de oro.
Consideremos un pentágono regular en el cual se han dibujado las diagonales:
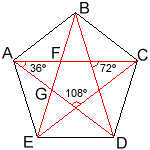
En esta figura sólo aparecen tres ángulos diferentes. Miden
,
y 
. La relación entre
estos ángulos es la
siguiente: 72 es el doble
de 36 y 108 es el triple de 36. Hay varios tipos diferentes de
triángulos isósceles, de los cuales seleccionamos
sólo tres:
los triángulos
, 
y 
. El resto de
los triángulos son semejantes a alguno
de estos
y no aportan información adicional. Finalmente, hay cuatro
segmentos
diferentes en estos triángulos, que llamaremos: 
, 
,
y 
.Las longitudes de estos segmentos cumplen que :
.Consideremos ahora cada uno de estos triángulos por separado y apliquemos el teorema del seno.
El
:
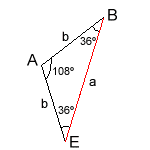
.El
:
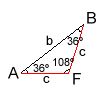
.El
:
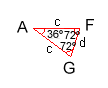
.La última igualdad se obtiene de que
y por tanto 
.En consecuencia podemos establecer que se tienen las siguientes proporciones:
.Es decir, una vez ordenadas las longitudes de los cuatro segmentos de mayor a menor, la razón entre cada una de ellas y la siguiente es igual a una constante, la pregunta que surge es entonces:
¿Cuál
es esta constante?
Y la respuesta es muy sencilla:
Tomando en cuenta que
y que todo lo que hemos calculado
anteriormente no depende del lente con el que hemos mirado nuestra
figura, podemos ajustar nuestro lente para que el lado 
mida
con lo cual el valor de nuestra constante será igual
al valor de 
, el que podemos calcular fácilmente; en
efecto:
.Es decir, dos de estos segmentos consecutivos cumplen la proporción áurea.
Como consecuencia, se verifica también que
