|
Temas: Matemáticas. Naturaleza. Arte. Mapa del sitio. Mail. |
 |


5 Aplicación
5.1 Simetría e invariabilidad ante transformaciones.
Habitualmente, el término simetría se utiliza para designar una suerte de ``buena proporción" entre las diversas partes que constituyen un todo. En este sentido, la simetría se asocia a algún tipo de equilibrio en la manera en que distintos elementos se integran para formar un objeto, y se le suele asociar con la belleza en las formas de la naturaleza y en el arte.
Un ejemplo importante de simetría es la bilateral, que en términos generales se puede describir diciendo que si la mitad de la izquierda se refleja en un espejo entonces se obtiene la de la derecha. De esta forma, una forma que posee simetría bilateral permanece invariable cuando se realiza una reflexión en torno a su eje.
Este ejemplo sugiere que una forma de formalizar matemáticamente la noción de simetría consiste en estudiar las transformaciones que dejan invariable el objeto en observación.
Una transformación es una regla para realizar movimientos de objetos. Estos movimientos pueden ser rígidos : rotaciones, traslaciones y reflexiones. Una dilatación es un cambio de escala dado por una expansión o una contracción uniforme en torno a algún punto fijo determinado que se denomina centro de la dilatación.
Si la forma de un objeto permanece invariable luego de aplicarle una transformación dada, entonces decimos que posee la simetría asociada a dicha transformación. Por ejemplo, si a un círculo se le aplica una rotación en un ángulo arbitrario en torno a su centro, se conserva la forma del círculo. Todo objeto con esta propiedad se dice que posee simetría circular.
Veamos que las rotaciones, traslaciones y reflexiones pueden ser
vistas como acciones de grupos.
Nota: Desde ahora el objeto en cuestión será un
conjunto acotado de ![]() .
.
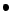
- Rotaciones.
Primero notemos que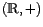 es un grupo abeliano. Sea
es un grupo abeliano. Sea
 la
relación dada por
Claramente
la
relación dada por
Claramente
 es
una relación de equivalencia compatible con
es
una relación de equivalencia compatible con  . Luego podemos hablar del grupo
cociente
. Luego podemos hablar del grupo
cociente  . Sea
. Sea 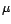 la
siguiente acción de
la
siguiente acción de  en
en
 .
.
Con




 .
. 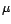 consiste en rotar en
un ángulo
consiste en rotar en
un ángulo  la componente
la componente  y en
un ángulo
y en
un ángulo  la componente
la componente  del vector
del vector  visto con coordenadas esféricas
visto con coordenadas esféricas
 .
.
Veamos que efectivamente se trata de una acción:-
 consiste en rotar
consiste en rotar  en el
neutro de
en el
neutro de  , el cual es el
, el cual es el
 , luego
, luego  no
sufre ninguna rotación, luego
no
sufre ninguna rotación, luego

-
 consiste en primero rotar
consiste en primero rotar  primero en el vector angular
primero en el vector angular
 ,
para luego rotarlo en vector angular
,
para luego rotarlo en vector angular
 ,
lo cual claramente es lo mismo que rotar
,
lo cual claramente es lo mismo que rotar  en el vector angular
en el vector angular  , el cual es la
operación en el grupo
, el cual es la
operación en el grupo
 de
de
 con
con
 .
Luego
.
Luego

-
- Traslaciones.
En este caso el grupo que usaremos será , y la acción
es
simplemente la acción de
, y la acción
es
simplemente la acción de  como conjunto sobre
como conjunto sobre
 como
grupo, es decir
como
grupo, es decir



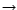
 .
.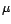 es claramente una acción.
Así
queda definida la acción
traslación.
es claramente una acción.
Así
queda definida la acción
traslación. 
- Reflexiones.
Para hablar de reflexión , primero debemos considerar que se entiende por reflexión. La idea del reflejado con respecto a un eje nos da la idea de como definirla de manera conveniente. La reflexión será entendida como sigue: Dado un hiperplano , la reflexión
de
, la reflexión
de  seria el reflejado del
vector sobre el hiperplano. Sin perdida de generalidad podemos
suponer que son hiperplanos que pasan por el origen, ya que una
reflexión por un hiperplano
seria el reflejado del
vector sobre el hiperplano. Sin perdida de generalidad podemos
suponer que son hiperplanos que pasan por el origen, ya que una
reflexión por un hiperplano  cualquiera puede ser
entendida
como una traslación en
cualquiera puede ser
entendida
como una traslación en  combinada con una
reflexión por
hiperplano
combinada con una
reflexión por
hiperplano  que pasa por el origen. Claramente
se
debe tener que
que pasa por el origen. Claramente
se
debe tener que  . Ahora tenemos
que dar una definición del reflejado de
. Ahora tenemos
que dar una definición del reflejado de  con
respecto a
un hiperplano
con
respecto a
un hiperplano  que pasa por el origen. La
reflexión de
que pasa por el origen. La
reflexión de  sobre
sobre
 es un vector
es un vector  tal
que en la componente según
tal
que en la componente según  , la
normal del
hiperplano
, la
normal del
hiperplano  , tenga el signo opuesto que la
componente según
, tenga el signo opuesto que la
componente según  del vector
del vector  , mientras que la componente de
, mientras que la componente de  sobre
sobre  se mantiene constante.
se mantiene constante.
Como estamos suponiendo que los hiperplanos pasan por el origen, el único dato relevante es la normal al hiperplano. Claramente el conjunto de todas las normales de todos los hiperplanos que pasan por el origen es .
La siguiente es una acción de
.
La siguiente es una acción de  (como grupo) sobre
(como grupo) sobre  (como conjunto)
Donde
(como conjunto)
Donde
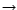


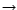
 .
. consiste en cambiar de signo la
componente
consiste en cambiar de signo la
componente  de
de  .
Mas explícitamente
Si
.
Mas explícitamente
Si con
con