



Next: Structures de données
Up: LEÇON Un programme d'Elements
Previous: Introduction
Comme il s'agit d'un problème de minimisation sans contrainte, on peut
utiliser l'algorithme suivant dans lequel  désigne le nombre de
sommet de la triangulation:
désigne le nombre de
sommet de la triangulation:
- 0 choisir la précision epsilon, le nombre maximal d'iterations mMax,
choisir une initialisation
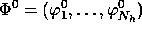 de
de 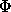 vérifiant
vérifiant 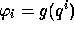 pour tout sommet du bord,
poser m=0,
pour tout sommet du bord,
poser m=0,  avec
avec
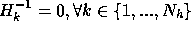 et définir
et définir  ;
;
- 1 calculer, pour tous les indices
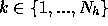 ,
,
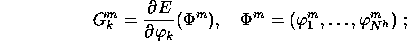
poser 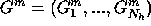 et définir
et définir
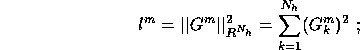
- 2 calculer
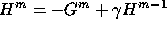 , où
, où 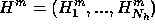 ,
avec
,
avec
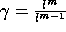 ;
;
- 3 poser
 , puis calculer le réel
, puis calculer le réel  qui minimise sur R la fonction
qui minimise sur R la fonction 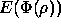 ;
;
- 4 Poser
 , incrémenter m de 1 et retourner
à l'étape 1 jusqu'à ce que
, incrémenter m de 1 et retourner
à l'étape 1 jusqu'à ce que 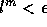 ou m>mMax (dans ce cas,
écrire que le programme ne marche pas).
ou m>mMax (dans ce cas,
écrire que le programme ne marche pas).
La valeur minimale  recherchée se calcule
explicitement par la résolution d'une équation du deuxième degré car
E est quadratique et nous obtenons
recherchée se calcule
explicitement par la résolution d'une équation du deuxième degré car
E est quadratique et nous obtenons

où le symbole  désigne le produit scalaire associé à la norme euclidienne.
désigne le produit scalaire associé à la norme euclidienne.
On rappelle que
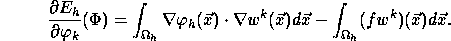
Pironneau Olivier
Jeudi 12 mars 1998 16:24:39
![]() désigne le nombre de
sommet de la triangulation:
désigne le nombre de
sommet de la triangulation:
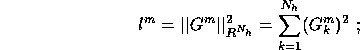
![]() recherchée se calcule
explicitement par la résolution d'une équation du deuxième degré car
E est quadratique et nous obtenons
recherchée se calcule
explicitement par la résolution d'une équation du deuxième degré car
E est quadratique et nous obtenons
![]()
![]() désigne le produit scalaire associé à la norme euclidienne.
désigne le produit scalaire associé à la norme euclidienne.
![]()