Pour résoudre le système linéaire A x=b, la méthode
de Gauss-Seidel consiste à définir par récurrence une suite de valeurs
pour 
, convergeant vers x, en résolvant
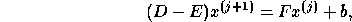
où nous avons utilisé la décomposition suivante de A :
A=D-E-F, avec D matrice diagonale dont les éléments diagonaux sont
ceux de A, -E matrice triangulaire inférieure stricte, dont les éléments
non nuls sont ceux de la partie triangulaire inférieure stricte de A et
-F=A-D+E partie triangulaire supérieure stricte de A.
La théorie nous dit que si la matrice A est symétrique définie positive
(ce qui est précisément le cas ici), cette méthode est convergente, dans
le sens où quand le nombre d'itérations j devient très grand, l'erreur
entre la solution exacte x et la solution approchée tend vers 0.
La programmation de cet algorithme pour la résolution du système
consiste à extraire la valeur de Tm de
l'équation m, ce qui donne :
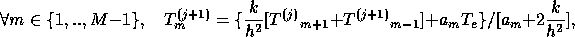
T0 et TM étant donnés.
Remarquons que l'indice j de l'itération de Gauss-Seidel n'est pas nécessaire
dans la programmation qui peut se faire en rangeant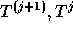 
dans la même mémoire. En effet, il n'est pas
nécessaire de stocker en mémoire les vecteurs correspondant à 2
itérations successives. Au fur et à mesure du calcul ( ie. quand
m augmente) la valeur de Tm à l'itération j est remplacée
par sa nouvelle valeur à l'itération j+1.
Cet algorithme est itéré autant de fois que nécessaire, ie. jusqu'à ce que les valeurs de Tm à deux étapes successives soient presque les mêmes.