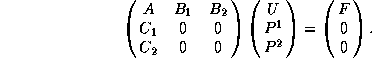
where the vector
At first sight, it seems difficult to use the vector programming technique for this element for which the number of unknowns at each node depends on the node position, whether at a vertex or at a mid-edge. However, by using an analogy with the hierarchical basis method of Yserantant[5] we can convert this problem into a vector problem.
We shall work with only one mesh, the velocity mesh, but we remember that it is a subdivision of a coarser mesh, the pressure mesh. The vertices of the coarse mesh will be called the P1 node and the other nodes (vertices of the fine mesh but not of the coarse mesh) the P2 nodes; We shall need a boolean function p2node(i) to tell if node i is P2 or P1.
Then let us denote the linear system of the P1-P1
element on the fine mesh without bubble stabilization by
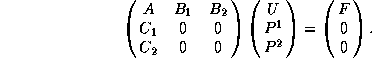
where the vector ![]() consists of all the values of the pressure at the coarse mesh (P1
nodes), and P¨2 those at the other (P2) nodes.
In view of the P1-iso-P2/P1 element three things are wrong with this system:
consists of all the values of the pressure at the coarse mesh (P1
nodes), and P¨2 those at the other (P2) nodes.
In view of the P1-iso-P2/P1 element three things are wrong with this system:
It is not hard to see that a cure to the first 2 problems can be given by defining
an upper triangular matrix L which has ones on its diagonal and such that

Then
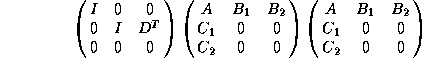
is the correct matrix for the P1-iso-P2/P1 element. However it is singular because the
P2-pressure degree of freedom are useless (problem 3).
One way is to replace the last block by the identity
matrix, but the correct values of the pressure at these places must be calculated once the
values of the pressure at the P1 nodes are known.