On se propose de résoudre en parallèle l'EDP
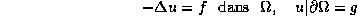
On dispose pour cela d'un générateur de maillage (freefem) et d'un solveur
éléments finis (delta.f).
Le solveur lit une triangulation d'un fichier, construit la matrice du système
linéaire et le résout par une méthode itérative (gradient conjugué
préconditioné).
Méthode avec recouvrement
Le domaine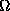 
est l'union 
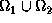telle que 
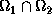soit non vide. La partie de frontière de 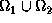qui est strictement
à l'intérieur de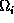 
sera notée 
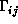(i,j=1,2).
L'algorithme consiste à boucler en m sur
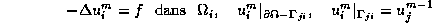
avec i=1,2.
On construira donc 2 triangulations, une pour chaque 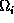, soit
directement (plus facile), soit à partir
d'une triangulation unique de 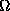(plus difficile mais plus élégant)
avec deux frontières internes. On pourra
utiliser l'indicateur de région, "region", défini par freefem pour chaque
triangle (voir doc de freefem). Il faudra alors extrère les 2 triangulations
de la triangulation globale. Dans les 2 cas
Il faudra ensuite construire un tableau de correspondance des numéros des
sommets de 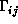d'une triangulation à l'autre (utiliser le numéro
des frontières et un test sur les coordonnées des points).
Méthode sans recouvrement
Le domaine est l'union de 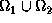mais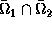 
est réduit à une frontière 
.
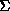L'algorithm consiste à boucler en m sur
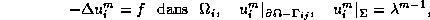
avec i=1,2 et, pour un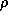 
fixe choisi à l'initialisation et un choix de
normale n, déterminant le signe de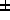 
dans la formule suivante
(voir le calcul 1D du cours):
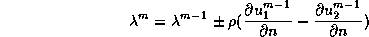
L'implémentation se fait comme dans la méthode avec recouvrement et là aussi
on a le choix entre deux méthodes pour construire les triangulations de
.
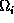Amélioration du solveur
Si le temps le permet, on pourra remplacer les itérations de point fixe
par des itérations de gradient conjugué pour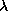 
. Et si vous avez
encore plus de temps vous pouvez préconditionner le gradient conjugué.