Trazado de una función de 2 variables

Principio: Interpolación P1

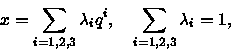
Si el dominio de la función f es triangulado, lo mas razonable es aproximar la función por su "interpolada P1", es decir, la única función que sea

• continue,
• afin en cada triángulo
• igual a f en los vértices de la triangulacion.

Théorème 1  

La interpolada P1 de una función continue es dafinida de manera única por sus valeurs en los vértices de la triangulacion.

Démonstration

Sea x un punto en el intérior del triángulo T dado por sus coordenadas baricentricas:

$$x=\sum _{i=1,2,3}\lambda _{i}q^{i},\quad \sum _{i=1,2,3}\lambda _{i}=1,$$

se define el valor de la interpolada P1 en x por

$$f_{h}(x)=\sum _{i=1,2,3}\lambda _{i}f(q^{i}).$$

Si x esta sobre una arista, se define la interpolada por

$$f_{h}(x)=\alpha f(q^{i})+(1-\alpha )f(q^{j}),\quad \textrm{donde}\; x=\alpha q^{i}+(1-\alpha )q^{j}.$$

Se ve fácilmente que la definición interna coincide con la definición en las aristas ya que si x tiende a una arista, una de las coordenadas barycentriques tiende a cero.

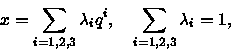
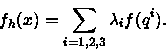
Las lineas de nivel de f son

$$L_{\mu }=\{x:f(x)=\mu \}.$$

Si se reemplaza f por su interpolada, las lineas de nivel seran lineas poligonales, ya que sobre cada triángulo son segmentos de recta, ya que la función es afin.

Un punto de intersection q de la curva de niveau con una arista del triángulo sera encontrada si existe i,j y a, con

$$e=[q^{i},q^{j}],\; q=aq^{i}+(1-a)q^{j},\quad f_{h}(q)=af_{h}(q^{i})+(1-a)f_{h}(q^{j})=\mu ,\quad 0\leq a\leq 1.$$

El principio de trazado de una linea de nivel es por lo tanto el siguiente:

for(int k = 0; k<nt; k++)
{
    m=0;
    for(int i1=0;i1<3;i1++)
    {
        int j1 = (i1+1)%3; 
        int i = t[k].v[i1]->no;
        int j = t[k].v[j1]->no;
        float a = (mu - f[j]) / (f[i] - f[j]);
        if((a>=0)&&(a<=1)) 
        {  
            m++; 
            if(m==1) 
                move2(a*q[i].x + (1-a)*q[j].x, 
                      a*q[i].y + (1-a)*q[j].y);
            else  
                line2(a*q[i].x + (1-a)*q[j].x, 
                      a*q[i].y + (1-a)*q[j].y);
        }
    }
}

A este programa conviene egregarle la verificación que los denominadores no son nulos, que la función no es identicamente constante, y agregarle el trazado de las fronteras del domaine.

EXERCICE 3   (Obligatoire)

Escribir un programa que lea un archivo freefem de triangulacion y un archivo de valeurs d'une función y escriba un archivo gnuplot con el trazado de las lineas de nivel. Debera testearse la presencia de 2 parametros en la linea de comandos UNIX. Si hay solo un parametro, debera trazarse la triangulacion en lugar de la función

Estimaciones de error

Se demuestra que el error H1 entre la interpolada y la función es O(h) mientras que el error L2 es O(h²).

EXERCICE 4  

Tomar 3 triangulaciones teniendo cada una 4 veces más puntos que la anterior, escribir una función que calcule el error H1 y L2 en el caso particular en que f=xy. Hacer con gnuplot un gráfico del log del error en función del log de h. Guardar la figura en formato Postscript y enviar el resultado comprimido por email.