 |
Temas: Matemáticas. Naturaleza. Arte. Mapa del sitio. Mail. |
 |
Construcción
de caracolas.
Construcción de la caracola del Nautilus.
La siguiente presentación está basada en la página de V.L.Hansen.
Recordemos algunos conceptos acerca de la espiral logaritmica.
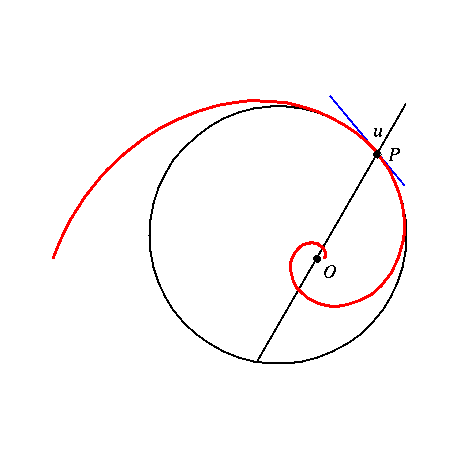
Un espiral logaritmico se caracteriza totalmente por ser una curva plana donde el vector tangente en cada punto
de la curva
tiene un ángulo constante 
con respecto a la
dirección radial, que parte de un punto fijo 
(origen
de la espiral) hacia el el punto . Por esta razón al
espiral logarítmico se le suele llamar espiral equiangular. Se
puede apreciar esto en la siguiente figura:
En cada punto de una curva plana, en particular en cada punto de la espiral logarítmica, existe un circulo que está definido como el mejor circulo que aproxima a la curva: éste es el famoso circulo de curvatura, con centro en
llamado el centro
de curvatura. Su construcción se puede apreciar en la
siguiente figura:
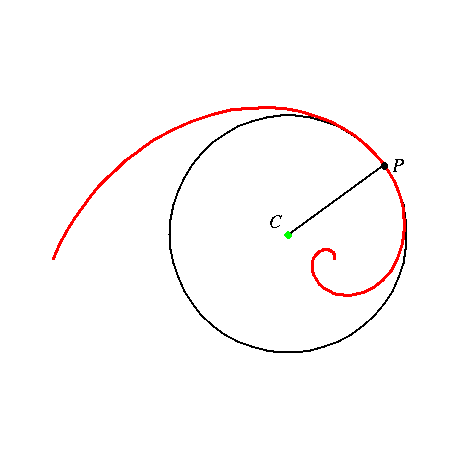
Los centros de la curvatura forman una nueva curva, la cual se llama la evoluta de la curva; la curva verde en la siguiente figura. Para el espiral logarítmico, sorprendentemente, la evoluta es otra vez un espiral logarítmico. Ésta puede ser construida rotando el espiral logarítmico en
y
multiplicando su radio por 
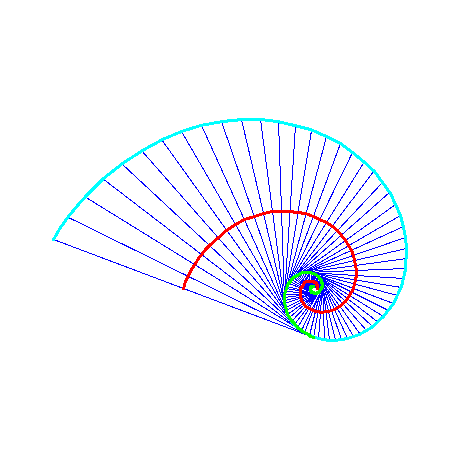
.Simétrica a la evoluta con respecto a la espiral logarítmica, existe otra espiral logaritmica, la cual se llama evoluta exterior. La evoluta exterior se representa en la siguente figura (curva celeste) junto con algunas tangentes a la evoluta que se conectan con puntos correspondientes a la evoluta exterior.
Existe un ángulo
,
aproximadamente el 
, para el cual la
evoluta y la evoluta exterior del
espiral logarítmico calzan, como se muestra en la siguiente
figura. En adelante, usaremos sólamente éste
ángulo para la espiral logarítmica.
Si los círculos de curvatura de la espiral logarítmica se trasladan a la curva en dirección radial , de tal forma que sus centros se encuentren ahora en la misma curva, y luego se rota, de tal forma que sean othogonales a la curva y al plano donde vive de la curva (ver animación), entonces una caracola de Nautilus aparece. Esto se puede observar en las figuras siguientes:
El
está muy cerca
de mitad del ángulo de oro
(aproximadamente de 
), que se presenta al
dividir el perimetro de un circulo en la proporción áurea.
Para el espiral logarítmico, dentro de la caracola
del Nautilus, es entonces aproximadamente cierto que la línea
que atraviesa el
origen y el punto de la curva , divide al
círculo de curvatura en el
cociente
de oro, como se muestra en la siguiente figura:
Otra cosa que hay que tener en cuenta es que el ángulo levemente más pequeño que
dado
por la mitad del ángulo de oro dejará un boquete entre la
evoluta y la evoluta exterior. Tal boquete permitirá el grueso
de la
cáscara de
Nautilus lo que apoya la conjetura de que el cociente de oro
está
conectado con este fenómeno de crecimiento en naturaleza.La mitad inferior y la mitad superior de la cáscara de Nautilus se muestran en las siguientes figuras:
