 |
Temas: Matemáticas. Naturaleza. Arte. Mapa del sitio. Mail. |
 |
Las
espirales en 2D.
La espiral de Cotes.
La espiral de Cotes es una espiral que da la solución al problema de orbitas centrales bajo una fuerza radial (o central)
 |
(1) |
donde
es una constante positiva.Hay tres soluciones al problema:
son constantes, |
 |
 |
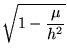(2) |
 |
|
 |
(3) |
y h es el momento angular específico (Whittaker 1944, p. 83).
El caso
da una epiespiral , mientras que
da
una espiral hiperbólica .
La Epiespiral.
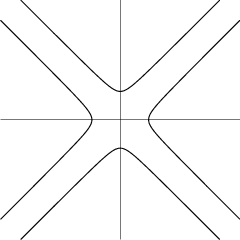
Es una curva plana de ecuación
Posee n secciones si n es impar y
si
n es par.Espiral de Cornu.
 |
(4) |
donde existen las integrales S (t) y C (t) de Fresnel (von Seggern 1993, p. 210; Gris 1997, p. 65). El espiral de Cornu también se conoce como el clothoid o espiral de Euler.Fue probablemente primero estudiado por Johann Bernoulli alrededor de 1696 (Bernoulli 1967, pp. 1084-1086). Un espiral de Cornu describe la difracción del borde de un semi-plano .
Las cantidades
y 
se
trazan arriba.
La cuesta del vector de la tangente de la curva (sobre figura derecha) es
 |
(5) |
trazado abajo.
La ecuación de Cesàro para un espiral de Cornu es
, donde 
está el radio de la
curvatura y s
la longitud
del arco .La torsión es
.
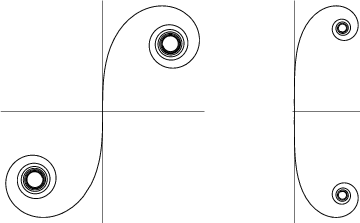
Gray (1997) define una generalización del espiral de Cornu dads por ecuaciones paramétricas
 |
|
 |
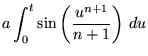(6) |
|
 |
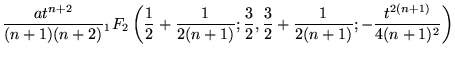(7) | |
 |
|
 |
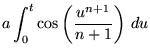(8) |
|
 |
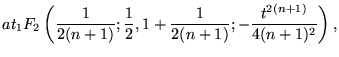(9) |
donde
es una función
hipergeométrica generalizada
La longitud del arco , la curvatura , y el ángulo tangencial de esta curva son
 |
|
 |
(10) |
 |
|
 |
(11) |
 |
|
 |
(12) |
La ecuación de Cesàro es
 |
(13) |
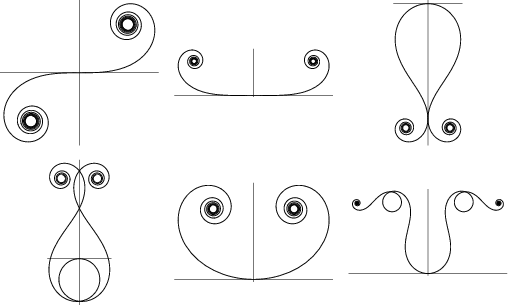
Dillen (1990) describe una clase de "espirales polinómicos" para cuál es una función la curvatura polinómica de la longitud del arco . Estos espirales son otra generalización del espiral de Cornu. Las curvas que se trazaron arriba corresponden a
, 
, 
, 
,
, y 
,
respectivamente.Circulo Espiral.
El espiral del círculo primero fue estudiado por Huygens cuando él consideraba los relojes sin el pendulo para el uso en las naves en el mar. Él utilizó el círculo espiral en su primer reloj del péndulo en una tentativa de forzar el péndulo para hacer pivotar en la trayectoria de una cicloide. Para un círculo de radio a = 1, las ecuaciones paramétricas del círculo y sus derivados son :
 |
(14) |
 |
(15) |
El vector de la tangente es
 |
(16) |
y la longitud del arco a lo largo del círculo está dada por :
 |
(17) |
la espiral se da tan cerca
 |
(18) |
Para un círculo con el radio a , por lo tanto sigue que la ecuación paramétrica del espiral está dada por
 |
 |
 |
(19) |
 |
|
 |
(20) |
La longitud del arco , la curvatura , y el ángulo tangencial son
 |
|
 |
(21) |
 |
|
 |
(22) |
 |
|
 |
(23) |
Su ecuación de Cesàro es
 |
(24) |
Daysies.
Una figura que se asemeja a una margarita o girasol en los cuales las copias de una figura geométrica del tamaño de aumento se ponen en los intervalos regulares a lo largo de un espiral. La figura que resulta aparece tener espirales múltiples el separarse hacia fuera del centro.
Espirales Inversas.
Dado un círculo M con el centro O y el radio k , entonces dos puntos de P y Q son inversos con respecto a C si
.Si P describe una curva , entonces Q describe una curva llamada la inversa con respecto al círculo M (de centro de la inversión O). El inversor de Peaucellier se puede utilizar para construir una curva inversa de una curva dada.
Si
es la ecuación polar de
la curva C
, entonces la
curva inversa tiene ecuación polar |
(25) |
Si
y 
,
entonces la inversa tiene ecuaciones |
 |
 |
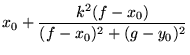(26) |
 |
|
 |
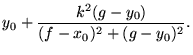(27) |
| Curva (espiral) | Centro de la inversión | Curva Inversa |
|---|---|---|
| Espiral de Arquímedes | origen | Espiral de Arquímedes |
| círculo | cualquier punto | otro círculo |
| cochleoid | origen | quadratrix de Hippias |
| Espiral de Fermat | origen | lituus |
| epiespiral | origen | Rose |
| lituus | origen | Espiral de Fermat |
| quadratrix de Hippias | origen | cochleoid |
| espiral sinusoidal | origen | espiral sinusoidal |
La curva inversa de las espirales Arquímedianas:
con el centro de la inversión en el radio del origen y de la inversión k es el espiral de Arquímedes
Tomando el origen como el centro de la inversión , el espiral de Archimedes
invierte al espiral hiperbólico
.
La curva inversa del epispiral
con el centro de la inversión en el radio del origen y de la inversión k es la Rose
