Discretization in space

In variational form it is: find with

Discretized by FEM of degree 1 it is: find such that

with

where T is any triangle of a triangulation of and where is the union of these triangles.

The solution is written on the basis of hat functions:

where denotes the vertices of the triangulation and the summation extends to INNER vertices only, because u is zero on the boundary. We obtain

where the U are vectors of values of u on vertices for all i,j corresponding to inner vertices.

The template for this algorithm is

  initialize or read data: grid g, u0, u1, dt...
  initialize U0 and U1
  loop on n
  {    Compute BU1
       Compute AU0
       Solve AU = 2(BU1) - AU0
       do U0=U1, U1=U
  }
  Write U on file for graphic display.

The initialization step is done as before:

#include <math.h>
#include <stdlib.h>
#include <iostream.h>
#include <fstream.h>
#include <assert.h>
#include "aarray.h"
#include "grid.h"

const int itermax = 100;
void main()
{
	float dt = 0.1;
	Grid g("square.msh");
	A<float> u0(g.nv), u1(g.nv), u(g.nv);
...

Here to compute BU there is no need to use mass lumping, we can use an exact formula:

which is also

It is programmed by "assembling" the contributions triangle by triangle. Note that it is easier to extend the array u to boundary vertices and put these extra values to zero rather than test the field g.v[i].where.

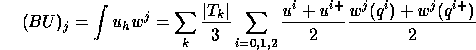
void bMul(A<float>& bu,  Grid& g,  A<float>& u)
{
      for(int i=0; i<g.nv; i++)
         bu[i] = 0;

	     for(int k=0; k<g.nt;k++)
		      for(int iloc = 0; iloc < 3; iloc++)
		      {	int i  = g(k,iloc);
			       for(int jloc = 0; jloc<3; jloc++)
			          bu[i] += u[g(k,jloc)] * g.t[k].area / 12;
			       bu[i] += u[i] * g.t[k].area / 12;
        }
}

Similarly AU is computed as in the explicit scheme

void aMul(A<float>& au,  Grid& g,  A<float>& u, float dt22)
{
   for(int i=0; i<g.nv; i++)
        au[i] = 0;

	  for(int k=0; k<g.nt;k++)
	     for(int iloc = 0; iloc < 3; iloc++)
		    {	 int i  = g(k,iloc);
			      int ip = g(k,(iloc+1)%3);
			      int ipp= g(k,(iloc+2)%3);
			     for(int jloc = 0; jloc<3; jloc++)
			     {	 int j  = g(k,jloc);
				       int jp = g(k,(jloc+1)%3);
				       int jpp= g(k,(jloc+2)%3);
				       float aijk = ((g.v[jpp].x - g.v[jp].x)*(g.v[ipp].x - g.v[ip].x)
							                 +(g.v[jpp].y - g.v[jp].y)*(g.v[ipp].y - g.v[ip].y))
							                   /g.t[k].area/4;
         		au[i] += u[j] * (g.t[k].area * dt22/ 12 + aijk );
       	}
			     au[i] += u[i] * g.t[k].area * dt22/ 12 ;
		   }
}

where dt22 is dt*dt/2 and where aijk is the same as in the explicit scheme: