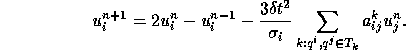Then Crank-Nicolson scheme for the time derivative is
In variational form it is
Discretized by the Finite Element method of degree 1 it is
with
where T is any triangle of a triangulation of 
and where 
is the union of these triangles.
The solution is decomposed on the basis of hat function:
where 
denotes the vertics of the triangulation. We obtain
Finally, using the mass lumping approximation for the first integral
where 
is the sum of the areas of the triangles which have qi as vertex and where
is a vector in the direction orthogonal to the base of 
opposite to 
and of length the distance between this vertex and this base.
Concretely, for a triangle
with vertices 
this vector is
Hence the scheme is written as
