Si l'on souhaite résoudre les systèmes linéaires par une méthode de Gauss il est indispensable de renuméroter les noeuds et éventuellement les éléments d'un maillage (méthode frontale).
De nombreuses méthodes existent pour effectuer ce type d'opérations. Nous allons décrire en détails la méthode de Gibbs qui est entièrement automatique et nous mentionnerons très brièvement d'autres approches.
Afin de pouvoir décrire cet algorithme, nous allons introduire (ou rappeler) les notations suivantes:
La renumérotation des noeuds, selon la méthode de Gibbs, comprend formellement trois étapes consistant en:
Nous allons maintenant détailler ces trois phases; en premier lieu nous définissons les notations supplémentaires suivantes:
Les trois phases consistent alors en:
Parmi les noeuds du contour du domaine, on sélectionne le noeud x tel que d(x) soit minimal.
Soient D(x) sa descendance et Np(x) son dernier niveau; on réalise alors l'algorithme suivant:
Le résultat nous donne un noeud y, extrémité d'un pseudo-diamètre dont l'autre extrémité x est un point du dernier niveau de la descendance de y tel que son degré soit minimal.
La phase deux de la méthode est alors entreprise:
x et D(x) = (N1(x),...,Np(x) )
y et D(y) = {N1(y),...,Np(y))
les descendances des points du pseudo-diamètre; on cherche à construire D=( N1,...,Np ) qui nous donnera la nouvelle numérotation des noeuds. Ce processus se décompose en plusieurs phases:
Boucle de w=1 à nv
Construction des couples (i,j) associés à w tels que:
(i,j) est formé si w est dans Ni(x) et w dans N(p+1-j)(y)
Fin de boucle.
Boucle de w=1 à nv
Si (i,j) associé à w existe:
mettre w dans Ni et retirer w du graphe G des noeuds
Fin de boucle.
Sinon on classe selon leur cardinal les t composantes connexes Ck du graphe G et on cherche à répartir les noeuds restants dans les niveaux Ni comme suit:
on calcule:
nm = card Nm
hm = nm + card (noeuds de Ck dans Nm(x) )
lm = nm + card (noeuds de Ck dans Nm(y) )
Fin de boucle.
Soient h0 = max(m=1...p)( hm tel que hm-nm positif ) et
l0 = max(m=1...p)(lm tel que lm-nm positif)
Ainsi une bonne répartition des noeuds est obtenue dans les différents niveaux.
Si d(y) est pus petit que d(x) , on échange x et y et on renverse les niveaux associés:
N(p-i+1) = Ni pour i=1...p
Notons NEW(x) le nouveau numéro correspondant à l'ancienne valeur n du noeud x. On pose:
NEW(x) = 1
Initialisation: n=1 et N0 = (x)
On boucle alors sur les p niveaux de la descendance:
a) tant qu'il existe w plus petit numéro des noeuds de Nk précédant des voisins non renumérotés,
faire: C(w) = voisins(w) intersecté avec N(k+1)
b) tant qu'il existe s de degré minimal de C(w) non renuméroté,
faire: n = n+1 et NEW(s) = n
Alors :
s = NEW(i)
NEW(i) =( nv+1 - s)
Fin de boucle
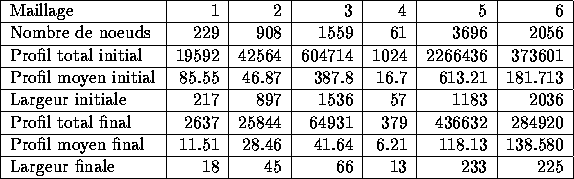
Cet algorithme est très performant pour réduire le profil d'une matrice, c'est-à-dire pour minimiser la différence entre les numéros des noeuds d'un même élément.
Pour illustrer cette propriété, nous allons donner quelques exemples. Nous introduisons les définitions suivantes:
Le profil total est la somme du nombre de colonnes (resp. lignes) comprises entre la première colonne (resp. ligne) non vide et la diagonale (dans le cas d'une matrice symétrique).
Le profil moyen est le quotient de cette valeur par le nombre de colonnes (lignes).
La largeur (ou largeur de bande) est le maximum des écarts entre la première colonne (ligne) remplie et la diagonale (dans le cas symétrique encore une fois). Cette largeur est la quantité que l'on cherche à minimiser dans le cas des méthodes de résolution directe.

Tableau 13.1 : Profil initial et profil après renumérotation.

Tableau : Renumérotation effectuée sur un maillage déjà renuméroté.