In this case the movement of two pendulums is modelled under the accion of gravity with applied forces.

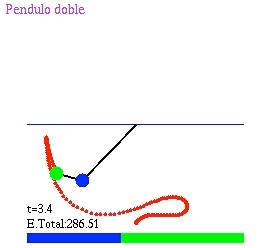
Secondly, a forced pendulum. Starting from the rest, the larger pendulum is forced with amplitude F1=20 and an eigenfrequency until t = 7, then with F2=100 applied on the smaller pendulum with another frequency... the result is the animation shown here.

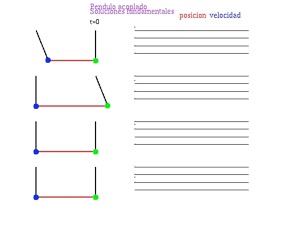
Here you can see other similar system of two coupled pendula connected by a spring. In this case the fundamental solutions for the linear case are shown.

For the derivation of the full nonlinear equations of the double pendulum see for example:

http://scienceworld.wolfram.com/physics/DoublePendulum.html

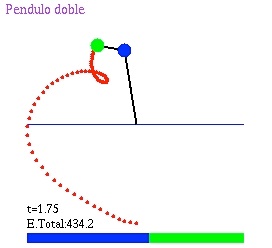
In the following simulations the full nonlinear system is modelled after reducing to a system of 4 equations (see the ode file for details).  We first consider the system subject to initial conditions but no applied forces. 

# nonlinear double pendulum

s12=sin(x1-x2)

c12=cos(x1-x2)

det = M2*L1*L2*(M1+M2*s12^2)

fu1 = 1/det*(M2*L2*F1*cos(w*t)-M2*L2*c12*F2*cos(w*t))

fu2 = 1/det*(-M2*L1*c12*F1*cos(w*t)+(M1+M2)*L1*F2*cos(w*t))

dx1/dt = y1

dy1/dt = M2*L2*g*(-sin(x1)*(M1+M2)+sin(x2)*M2*c12)/det-M2^2*L2*s12*(y2^2*L2+y1^2*L1*c12)/det+fu1

dx2/dt = y2

dy2/dt = M2*L1*g*(M1+M2)*(sin(x1)*c12-sin(x2))/det+M2*L1*s12*(y2^2*L2*M2*c12+y1^2*(M1+M2)*L1)/det + fu2