reservoirs in series and Jordan’s form

We consider 4 identical reservoirs connected in series. It is good example to understand the Jordan form of the underlying system. Water circulates with a diluted substance that is mixed instantly into each reservoir. The flow between the reservoirs is constant ¨b¨ so the volumes are preserved. There is also a deposition coefficient "sigma".
# Identical reservoirs in series
# example of Jordan form
# x[i]: specie in reservoir i [gr]
# V= volume [lt]
# b= volume flux [lt/seg]
# sigma = deposition coeff
# f = entry concentration [gr/lt]
# First reservoir...
x1'= -sigma*x1-b*x1/V+f*(1+cos(omega*t))*b
init x[1]=1
# and the other reservoirs...
%[2..4]
x[j]' = b*x[j-1]/V-sigma*x[j]-b*x[j]/V
init x[j]=0
# Parameters
param V=1, sigma=0.1
param b=1, f=0, omega=2
@ TOTAL=10
done
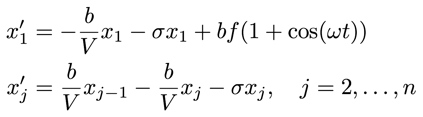
more about Jordan’s form:
We model the evolution for a periodic entrance of the substance. Initially, the first reservoir has a concentration 1 and the others 0.
This type of models are more generally called “compartimental models”, used in physiology, chemistry, ecology and biochemistry for instance.
more about compartimental modelling:


